directlabels - lineplot - Positioning Method - lines2

Positioning Method for 2 groups of longitudinal data. One curve is on top of the other one (on average), so we label the top one at its maximal point, and the bottom one at its minimal point. Vertical justification is chosen to minimize collisions with the other line. This may not work so well for data with high variability, but then again lineplots may not be the best for these data either.

lines2 <- function
### Positioning Method for 2 groups of longitudinal data. One curve
### is on top of the other one (on average), so we label the top one
### at its maximal point, and the bottom one at its minimal
### point. Vertical justification is chosen to minimize collisions
### with the other line. This may not work so well for data with high
### variability, but then again lineplots may not be the best for
### these data either.
(d,
### The data.
 offset=0.3,
### Offset from 0 or 1 for the vjust values.
 ...
### ignored.
 ){
  if(length(unique(d$groups))!=2)
    stop("need 2 groups for lines2")
  top <- 0-offset
  bottom <- 1+offset
  y <- gapply(d,get.means)
  gapply(y,function(D,...){
    bigger.on.average <- D$y==max(y$y)
    f <- if(bigger.on.average)max else min
    compare <- get(if(bigger.on.average)">" else "<")
    is.group <- d$groups==D$groups
    ld    <- d[is.group,]
    other <- d[!is.group,]
    find.closest.y <- function(x){
      closest.x.on.other.line <- which.min(abs(other$x-x))
      other[closest.x.on.other.line,"y"]
    }
    ld$other.yvals <- sapply(ld$x,find.closest.y)
    ld$diff <- abs(ld$y-ld$other.yvals)
    more.extreme <- compare(ld$y,ld$other.yvals)
    ld <- ld[which(more.extreme),] ## which since can have NA
    ld <- ld[ld$y==f(ld$y),]
    which.closest <- which.max(ld$diff)
    pos <- ld[which.closest,]
    transform(pos,vjust=if(bigger.on.average)top else bottom)
  })
}
bodyweight

bodyweight

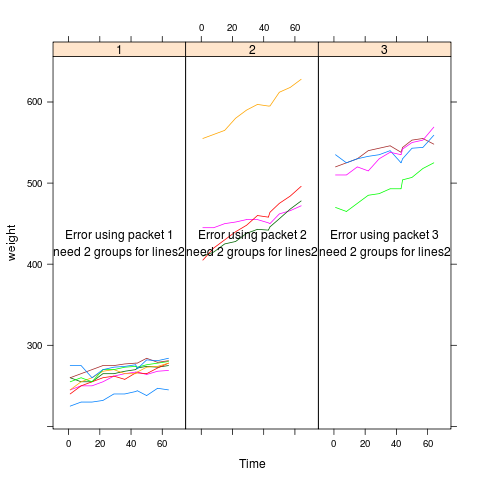
data(BodyWeight,package="nlme")
library(lattice)
p <- xyplot(weight~Time|Diet,BodyWeight,groups=Rat,type='l',
       layout=c(3,1),xlim=c(-10,75))
direct.label(p,"lines2")
chemqqmathscore

chemqqmathscore

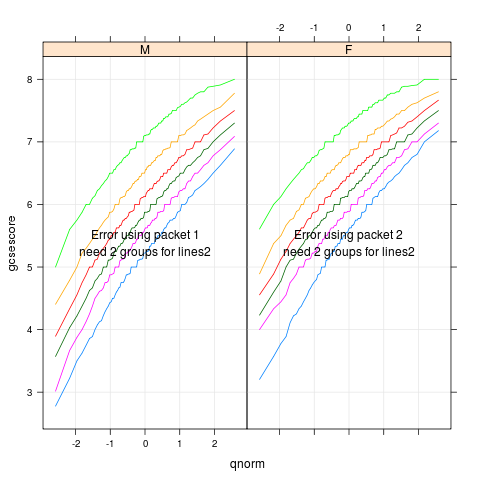
data(Chem97,package="mlmRev")
library(lattice)
p <- qqmath(~gcsescore|gender,Chem97,groups=factor(score),
       type=c('l','g'),f.value=ppoints(100))
direct.label(p,"lines2")
chemqqmathsex

chemqqmathsex

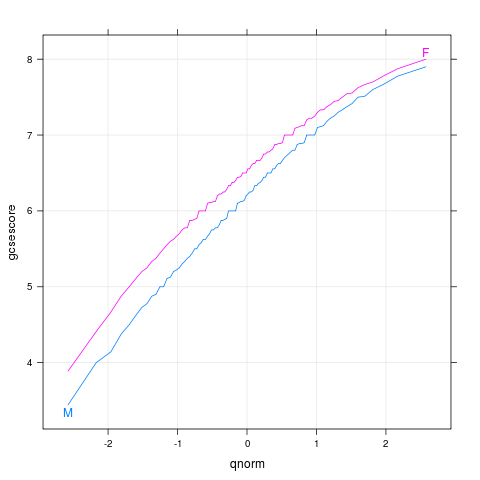
data(Chem97,package="mlmRev")
library(lattice)
p <- qqmath(~gcsescore,Chem97,groups=gender,
       type=c("l","g"),f.value=ppoints(100))
direct.label(p,"lines2")
lars

lars

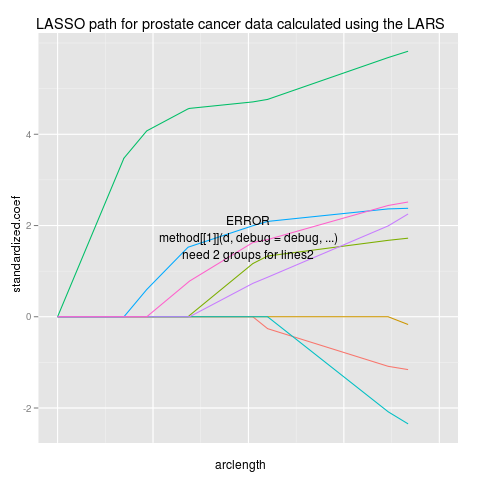
data(prostate,package="ElemStatLearn")
pros <- subset(prostate,select=-train,train==TRUE)
ycol <- which(names(pros)=="lpsa")
x <- as.matrix(pros[-ycol])
y <- pros[[ycol]]
library(lars)
fit <- lars(x,y,type="lasso")
beta <- scale(coef(fit),FALSE,1/fit$normx)
arclength <- rowSums(abs(beta))
library(reshape2)
path <- data.frame(melt(beta),arclength)
names(path)[1:3] <- c("step","variable","standardized.coef")
library(ggplot2)
p <- ggplot(path,aes(arclength,standardized.coef,colour=variable))+
  geom_line(aes(group=variable))+
  ggtitle("LASSO path for prostate cancer data calculated using the LARS")+
  xlim(0,20)
direct.label(p,"lines2")
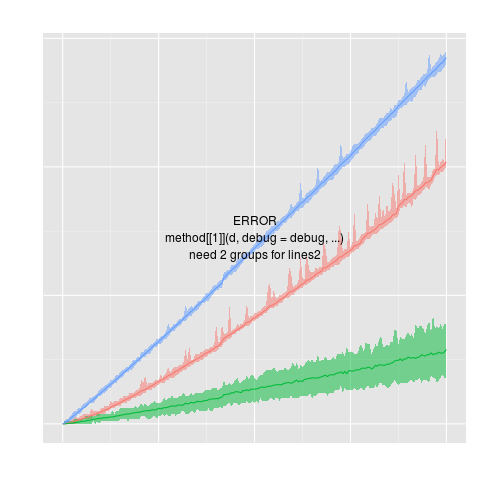projectionSeconds

projectionSeconds

data(projectionSeconds, package="directlabels")
p <- ggplot(projectionSeconds, aes(vector.length/1e6))+
  geom_ribbon(aes(ymin=min, ymax=max,
                  fill=method, group=method), alpha=1/2)+
  geom_line(aes(y=mean, group=method, colour=method))+
  ggtitle("Projection Time against Vector Length (Sparsity = 10%)")+
  guides(fill="none")+
  ylab("Runtime (s)")
direct.label(p,"lines2")
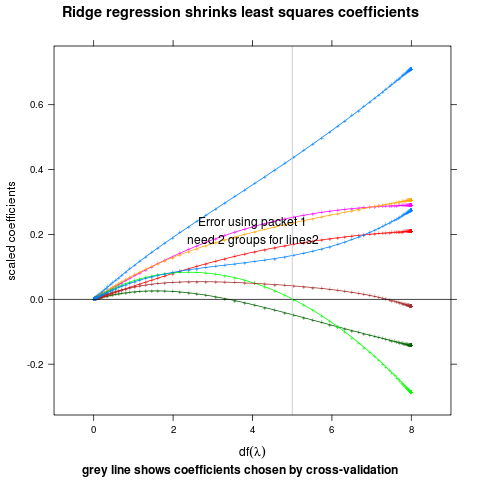ridge

ridge

## complicated ridge regression lineplot ex. fig 3.8 from Elements of
## Statistical Learning, Hastie et al.
myridge <- function(f,data,lambda=c(exp(-seq(-15,15,l=200)),0)){
  require(MASS)
  require(reshape2)
  fit <- lm.ridge(f,data,lambda=lambda)
  X <- data[-which(names(data)==as.character(f[[2]]))]
  Xs <- svd(scale(X)) ## my d's should come from the scaled matrix
  dsq <- Xs$d^2
  ## make the x axis degrees of freedom
  df <- sapply(lambda,function(l)sum(dsq/(dsq+l)))
  D <- data.frame(t(fit$coef),lambda,df) # scaled coefs
  molt <- melt(D,id=c("lambda","df"))
  ## add in the points for df=0
  limpts <- transform(subset(molt,lambda==0),lambda=Inf,df=0,value=0)
  rbind(limpts,molt)
}
data(prostate,package="ElemStatLearn")
pros <- subset(prostate,train==TRUE,select=-train)
m <- myridge(lpsa~.,pros)
library(lattice)
p <- xyplot(value~df,m,groups=variable,type="o",pch="+",
       panel=function(...){
         panel.xyplot(...)
         panel.abline(h=0)
         panel.abline(v=5,col="grey")
       },
       xlim=c(-1,9),
       main="Ridge regression shrinks least squares coefficients",
       ylab="scaled coefficients",
       sub="grey line shows coefficients chosen by cross-validation",
       xlab=expression(df(lambda)))
direct.label(p,"lines2")
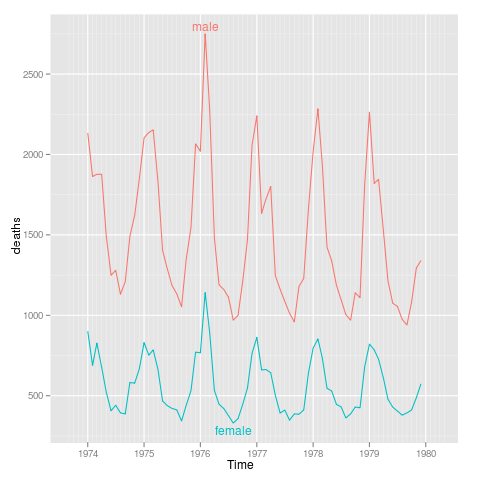sexdeaths

sexdeaths

library(ggplot2)
tx <- time(mdeaths)
Time <- ISOdate(floor(tx),round(tx%%1 * 12)+1,1,0,0,0)
uk.lung <- rbind(data.frame(Time,sex="male",deaths=as.integer(mdeaths)),
                 data.frame(Time,sex="female",deaths=as.integer(fdeaths)))
p <- qplot(Time,deaths,data=uk.lung,colour=sex,geom="line")+
  xlim(ISOdate(1973,9,1),ISOdate(1980,4,1))
direct.label(p,"lines2")
Please contact Toby Dylan Hocking if you are using directlabels or have ideas to contribute, thanks!
Documentation website generated from source code version 2021.2.24 (git revision bb6db07 Mon, 14 Jun 2021 22:38:45 +0530) using inlinedocs.
validate