Recently we proposed Same/Other/All K-fold cross-validation (SOAK), which generalizes the classic K-fold cross-validation procedure to data sets with qualitatively different subsets of interest (space, time, etc.). SOAK allows us to measure the extent to which it is beneficial to combine data subsets when training, and to use other data subsets to predict the test subset of interest (this is the heart of machine learning, generalization to new data).

While working as a professor at NAU, I wrote a chapter “Introduction to machine learning and neural networks” for Yiqi Luo’s textbook Land Carbon Cycle Modeling Matrix Approach, Data Assimilation, & Ecological Forecasting. In that chapter, I wrote definitions for different split sets (train/test/subtrain/validation).

  • Definition of train and test: “Each train set is used to learn a corresponding prediction function, which is then used to predict on the held out test data.”
  • Definition of subtrain and validation: “Then how do we know which hyper-parameters will result in learned functions which best generalize to new data? A general method which can be used with any learning algorithm is splitting the train set into subtrain and validation sets, then using grid search over hyper-parameter values. The subtrain set is used for parameter learning, and the validation set is used for hyper-parameter selection.”

The word “subtrain” is not very common, but it is quite useful, because it allows us to differentiate it from the train set. Where did I get that from?

My writing

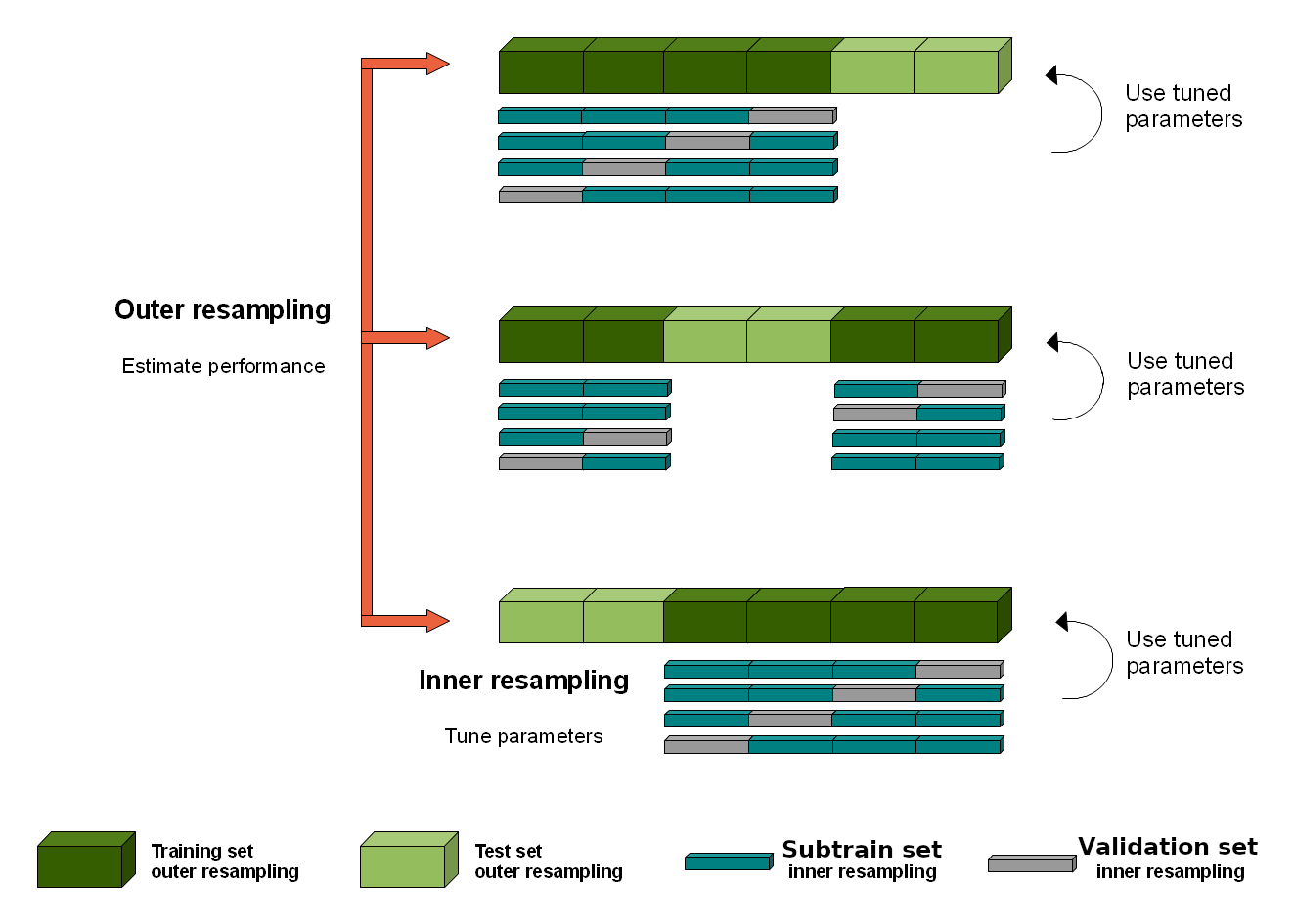
nested resampling

I adapted the figure above from this one in the mlr3 docs.

Below is a review of discussion of cross-validation in various other sources.

Does not mention subtrain

This section cites references that do not mention subtrain, although some mention that using “train” for two different sets is confusing.

Deep Learning, Goodfellow et al.

5.3 Hyperparameters and Validation Sets “We always construct the validation set from the training data. We split the training data into two disjoint subsets. One of these subsets is used to learn the parameters. The other subset is our validation set, used to estimate the generalization error during or after training, allowing for the hyperparameters to be updated accordingly. the subset of data used to learn the parameters is still typically called the training set, even though this may be confused with the larger pool of data used for the entire training process. The subset of data used to guide the selection of hyperparameters is called the validation set. Typically, one uses about 80 percent of the training data for training and 20 percent for validation. Since the validation set is used to “train” the hyperparameters, the validation set error will underestimate the generalization error, though typically by a smaller amount than the training error does. After all hyperparameter optimization is complete, the generalization error may be estimated using the test set”

Murphy MLAPP

Machine Learning: A Probabilistic Perspective (2012) says

1.4.8 Model selection. However, what we care about is generalization error, which is the expected value of the misclassification rate when averaged over future data sets (see Section 6.3 for details). This can be approximated by computing the misclassification rate on a large independent test set, not used during model training… Unfortunately, when training the model, we don’t have access to the test set (by assumption), so we cannot use the test set to pick the model of the right complexity. However, we can create a test set by partitioning the training set into two: the part used for training the model, and a second part, called the validation set, used for selecting the model complexity. We then fit all the models on the training set, and evaluate their performance on the validation set, and pick the best. Once we have picked the best, we can refit it to all the available data. If we have a separate test set, we can evaluate the performance on this, in order to estimate the accuracy of our method.

Hastie et al. ESL

7.2 Bias, Variance and Model Complexity. It is important to note that there are in fact two separate goals that we might have in mind:

  • Model selection: estimating the performance of different models in order to choose the best one.
  • Model assessment: having chosen a final model, estimating its prediction error (generalization error) on new data.

If we are in a data-rich situation, the best approach for both problems is to randomly divide the dataset into three parts: a training set, a validation set, and a test set. The training set is used to fit the models; the validation set is used to estimate prediction error for model selection; the test set is used for assessment of the generalization error of the final chosen model.

Russell and Norvig, AIMA

19.4 Model Selection and Optimization. Suppose a researcher generates a hypothesis for one setting of the chi-square pruning hyperparameter, measures the error rates on the test set, and then tries different hyperparameters. No individual hypothesis has peeked at the test data, but the overall process did, through the researcher.

The way to avoid this is to really hold out the test set—lock it away until you are completely done with training, experimenting, hyperparameter-runing re-training, etc. That means you need three data sets:

  • A training set to train candidate models.
  • A validation set, also known as a development set or dev set, to evaluate the candidate models and choose the best one.
  • A test set to do a final unbiased evaluation of the best model.

Bishop, PRML

1.3 Model Selection We have already seen that, in the maximum likelihood approach, the performance on the training set is not a good indicator of predictive performance on un-seen data due to the problem of over-fitting. If data is plentiful, then one approach is simply to use some of the available data to train a range of models, or a given model with a range of values for its complexity parameters, and then to compare them on independent data, sometimes called a validation set, and select the one having the best predictive performance. If the model design is iterated many times using a limited size data set, then some over-fitting to the validation set can occur and so it may be necessary to keep aside a third test set on which the performance of the selected model is finally evaluated.

Liquet, Moka, Nazarathy: Mathematical Engineering of Deep Learning

2.5 Generalization, Regularization and Validation The train-validate split approach simply implies that the original data with n samples is first split into training and testing as before and then the training data is further split into two subsets where the first is (confusingly) again called the training set and the latter is the validation set.

Rasmussen and Williams, GPML

5.3 Cross-validation The basic idea is to split the training set into two disjoint sets, one which is actually used for training, and the other, the validation set, which is used to monitor performance.

Do mention subtrain

These references do use subtrain, but it is not clear where that nomenclature comes from.

Solving Multiclass Learning Problems via Error-Correcting Output Codes

The training set is sub divided into a subtraining set and a validation set. While training on the subtraining set, we observed generalization performance on the validation set to determine the optimal settings of learning rate and network size and the best point at which to stop training. The training set mean squared error at that stopping point is computed, and training is then performed on the entire training set using the chosen parameters and stopping at the indicated mean squared error. Finally, we measure network performance on the test set.

Notes on data science for business

Let-s say we are saving the test set for a final assessment. We can take the training set and split it again into a training subset and a testing subset. Then we can build models on this training subset and pick the best model based on this testing subset. Let-s call the former the subtraining set and the latter the validation set for clarity. The validation set is separate from the final test set, on which we are never going to make any modeling decisions. This procedure is often called nested holdout testing.