Heap in R and python
Yesterday I was reading the source code for the scikit-learn function
that implements Hierachical clustering with Ward linkage,
_agglomerative.py. The
python function ward_tree() uses functions heapify(), heappop(),
heappush(). The heapify
docs say
that it converts a python list (~ C++ STL vector) to a min-heap. Is there an equivalent in R?
In theory
The basic data structures in R are “vectors” which are in fact more like C++ STL arrays (fixed size). So in R we could have a large heap that reduces in size (with some unused elements). If we had a small heap, and we wanted to increase its size, we could use the same trick that python uses to enable its “lists” to support the append operation (allocate a new array double the size and have some unused elements).
Software
In C++ STL there is make_heap() which works on any random access iterator (vector or array).
The heap is also used in the priority_queue data structure which I have used to implement efficient binary segmentation in binsegRcpp/src/binseg.cpp.
Of course we can call C++ from R or Python.
But can we call an R function like make_heap() in C++ or heapify() in python?
There was a datastructures CRAN package, now only on github:
remotes::install_github("dirmeier/datastructures")
## Using GitHub PAT from the git credential store.
## Skipping install of 'datastructures' from a github remote, the SHA1 (c69faa25) has not changed since last install.
## Use `force = TRUE` to force installation
For the application to hierarchical clustering, we want efficient minimization of numeric distances, so we create a heap with numeric keys below.
num_heap <- datastructures::fibonacci_heap("numeric")
datastructures::size(num_heap)
## [1] 0
Above we see that it starts empty (size 0). Below we insert five simulated distances as keys.
set.seed(1)
(dist.vec <- rnorm(5))
## [1] -0.6264538 0.1836433 -0.8356286 1.5952808 0.3295078
datastructures::insert(num_heap, dist.vec, 1:5)
## An object of class fibonacci_heap<numeric, SEXP>
##
## Peek: -0.835629 -> integer, ...
datastructures::size(num_heap)
## [1] 5
Above we see the size has increased to 5. Below we pop one item from the heap.
datastructures::pop(num_heap)
## $`-0.835629`
## [1] 3
datastructures::size(num_heap)
## [1] 4
Above we see that it popped the smallest distance, and the new size is 4. Below we adapt these methods to an atime performance comparison.
library(data.table)
a_result <- atime::atime(
setup={
set.seed(1)
keys <- rnorm(N)
values <- 1:N
},
data.frame={
df <- data.frame(keys, values)
out <- integer(N)
for(i in 1:N){
min.row <- which.min(df$keys)
df$keys[min.row] <- NA
out[[i]] <- df$values[min.row]
}
out
},
seconds=1,
result=TRUE,
heap={
num_heap <- datastructures::fibonacci_heap("numeric")
datastructures::insert(num_heap, keys, values)
out <- integer(N)
for(i in 1:N){
out[[i]] <- datastructures::pop(num_heap)[[1]]
}
out
})
plot(a_result)
## Warning in ggplot2::scale_y_log10("median line, min/max band"): log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.
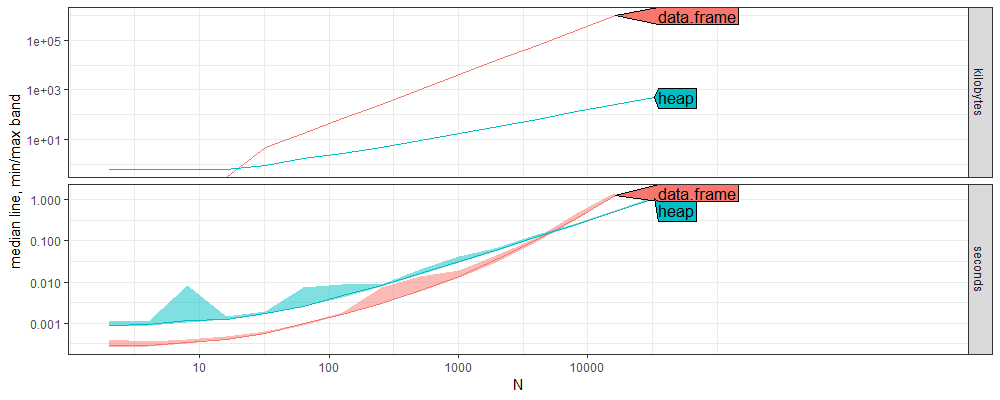
Above we see that
- for small data sizes, the linear search with a data frame is faster than the heap pop.
- for large data sizes, the heap pop is faster than the linear search with the data frame.
- the asymptotic time and memory usage (slope on the right) is smaller for heap, which indicates a smaller big-O complexity class.
Below we plot reference lines to estimate the big-O classes.
a_refs <- atime::references_best(a_result)
plot(a_refs)
## Warning in ggplot2::scale_y_log10(""): log-10 transformation introduced infinite values.
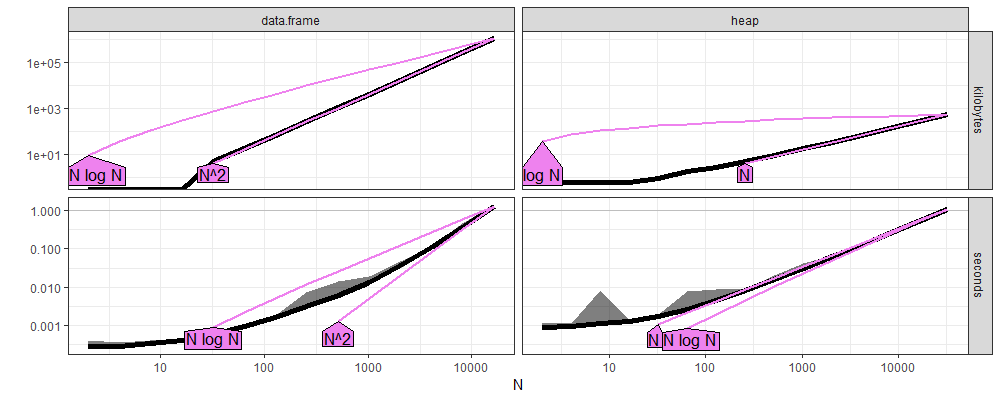
The plot above shows that
data.frameis quadraticO(N^2)time and memory.heapis log-linearO(N log N)time and linearO(N)memory.
These are the expected results from using a heap versus a vector.
Conclusions
We have shown that there is an R package datastructures which implements the heap, and has expected asymptotic time/space complexity.
Session info
sessionInfo()
## R version 4.4.1 (2024-06-14 ucrt)
## Platform: x86_64-w64-mingw32/x64
## Running under: Windows 11 x64 (build 26100)
##
## Matrix products: default
##
##
## locale:
## [1] LC_COLLATE=English_United States.utf8 LC_CTYPE=English_United States.utf8 LC_MONETARY=English_United States.utf8
## [4] LC_NUMERIC=C LC_TIME=English_United States.utf8
##
## time zone: America/Toronto
## tzcode source: internal
##
## attached base packages:
## [1] stats graphics utils datasets grDevices methods base
##
## other attached packages:
## [1] data.table_1.17.8
##
## loaded via a namespace (and not attached):
## [1] gtable_0.3.6 dplyr_1.1.4 compiler_4.4.1 crayon_1.5.3 tidyselect_1.2.1 Rcpp_1.1.0
## [7] datastructures_0.2.9 scales_1.4.0 directlabels_2025.6.24 lattice_0.22-7 ggplot2_4.0.0 R6_2.6.1
## [13] generics_0.1.4 curl_7.0.0 knitr_1.50 tibble_3.3.0 atime_2025.5.24 pillar_1.11.1
## [19] RColorBrewer_1.1-3 rlang_1.1.6 xfun_0.53 quadprog_1.5-8 S7_0.2.0 cli_3.6.5
## [25] withr_3.0.2 magrittr_2.0.4 grid_4.4.1 remotes_2.5.0 lifecycle_1.0.4 vctrs_0.6.5
## [31] bench_1.1.4 evaluate_1.0.5 glue_1.8.0 farver_2.1.2 codetools_0.2-20 profmem_0.7.0
## [37] purrr_1.1.0 tools_4.4.1 pkgconfig_2.0.3