Comparing pruning methods for optimal partitioning
The goal of this post is to compare two pruning methods for speeding up the optimal partitioning algorithm.
- We assume that we want to find change-points in a sequence of
Ndata. - All algorithms discussed are instances of dynamic programming, which
has a for loop over all
Ndata. In each iteration, the algorithm considers a certain number of candidate change-pointsC(on average). The algorithm is overallO(NC)time. - Optimal partitioning (OPART) computes the best segmentation for a
given loss function, data sequence, and non-negative penalty
value. Each iteration considers the loss for each previous candidate
change-point,
C=O(N)linear time per iteration, which implies quadraticO(N^2)time overall. - Pruned Exact Linear Time (PELT) reduces the number of candidate
change-points that must be considered at each iteration, from the
whole data sequence size
N, to the size of a segmentS, soC=O(S). This gives an algorithm which isO(NS)time overall.- If the number of change-points grows linearly with the data size
N, then the segment size is constant,S=O(1)with respect to number of dataN, and the PELT algorithm is indeed linear time overall,O(N). - However in the case of a constant number of change-points, with
segment sizes that grow with the data sequence,
S=O(N)implies quadratic time overall,O(N^2).
- If the number of change-points grows linearly with the data size
- Functional Pruning Optimal Partitioning (FPOP) reduces the number of
candidate change-points to a number which is always less than the
number considered by PELT (see Maidstone 2017 paper for detailed
proof). The goal of this post is to show that it prunes more than
PELT in both cases:
- If the number of change-points grows linearly with the data size
N, then both PELT and FPOP areO(N)overall. - If the number of change-points is constant with respect to data
size
N, then FPOP considers onlyS=O(log N)change-points (empirically), which gives an algorithm that isO(N log N), log-linear time overall.
- If the number of change-points grows linearly with the data size
Simulate data sequences
We simulate data in two scenarios: linear and constant number of changes.
mean_vec <- c(10,20,5,25)
sim_fun_list <- list(
constant_changes=function(N){
rep(mean_vec, each=N/4)
},
linear_changes=function(N){
rep(rep(mean_vec, each=25), l=N)
})
lapply(sim_fun_list, function(f)f(100))
## $constant_changes
## [1] 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 20 20 20 20 20 20 20 20 20 20 20 20 20
## [39] 20 20 20 20 20 20 20 20 20 20 20 20 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 25
## [77] 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
##
## $linear_changes
## [1] 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 20 20 20 20 20 20 20 20 20 20 20 20 20
## [39] 20 20 20 20 20 20 20 20 20 20 20 20 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 25
## [77] 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25 25
As can be seen above, both functions return a vector of values that represent the true segment mean. Below we use both functions with a three different data sizes.
library(data.table)
N_data_vec <- c(100,200,400)
sim_data_list <- list()
sim_changes_list <- list()
for(N_data in N_data_vec){
for(simulation in names(sim_fun_list)){
sim_fun <- sim_fun_list[[simulation]]
data_mean_vec <- sim_fun(N_data)
end <- which(diff(data_mean_vec) != 0)
set.seed(1)
data_value <- rpois(N_data, data_mean_vec)
sim_data_list[[paste(N_data, simulation)]] <- data.table(
N_data, simulation, data_index=seq_along(data_value), data_value)
sim_changes_list[[paste(N_data, simulation)]] <- data.table(
N_data, simulation, end)
}
}
addSim <- function(DT)DT[, Simulation := paste0("\n", simulation)][]
(sim_changes <- addSim(rbindlist(sim_changes_list)))
## N_data simulation end Simulation
## <num> <char> <int> <char>
## 1: 100 constant_changes 25 \nconstant_changes
## 2: 100 constant_changes 50 \nconstant_changes
## 3: 100 constant_changes 75 \nconstant_changes
## 4: 100 linear_changes 25 \nlinear_changes
## 5: 100 linear_changes 50 \nlinear_changes
## 6: 100 linear_changes 75 \nlinear_changes
## 7: 200 constant_changes 50 \nconstant_changes
## 8: 200 constant_changes 100 \nconstant_changes
## 9: 200 constant_changes 150 \nconstant_changes
## 10: 200 linear_changes 25 \nlinear_changes
## 11: 200 linear_changes 50 \nlinear_changes
## 12: 200 linear_changes 75 \nlinear_changes
## 13: 200 linear_changes 100 \nlinear_changes
## 14: 200 linear_changes 125 \nlinear_changes
## 15: 200 linear_changes 150 \nlinear_changes
## 16: 200 linear_changes 175 \nlinear_changes
## 17: 400 constant_changes 100 \nconstant_changes
## 18: 400 constant_changes 200 \nconstant_changes
## 19: 400 constant_changes 300 \nconstant_changes
## 20: 400 linear_changes 25 \nlinear_changes
## 21: 400 linear_changes 50 \nlinear_changes
## 22: 400 linear_changes 75 \nlinear_changes
## 23: 400 linear_changes 100 \nlinear_changes
## 24: 400 linear_changes 125 \nlinear_changes
## 25: 400 linear_changes 150 \nlinear_changes
## 26: 400 linear_changes 175 \nlinear_changes
## 27: 400 linear_changes 200 \nlinear_changes
## 28: 400 linear_changes 225 \nlinear_changes
## 29: 400 linear_changes 250 \nlinear_changes
## 30: 400 linear_changes 275 \nlinear_changes
## 31: 400 linear_changes 300 \nlinear_changes
## 32: 400 linear_changes 325 \nlinear_changes
## 33: 400 linear_changes 350 \nlinear_changes
## 34: 400 linear_changes 375 \nlinear_changes
## N_data simulation end Simulation
Above we see the table of simulated change-points.
- For
constant_changessimulation, there are always 3 change-points. - For
linear_changessimulation, there are more change-points when there are more data.
Below we visualize the simulated data.
(sim_data <- addSim(rbindlist(sim_data_list)))
## N_data simulation data_index data_value Simulation
## <num> <char> <int> <int> <char>
## 1: 100 constant_changes 1 8 \nconstant_changes
## 2: 100 constant_changes 2 10 \nconstant_changes
## 3: 100 constant_changes 3 7 \nconstant_changes
## 4: 100 constant_changes 4 11 \nconstant_changes
## 5: 100 constant_changes 5 14 \nconstant_changes
## ---
## 1396: 400 linear_changes 396 24 \nlinear_changes
## 1397: 400 linear_changes 397 20 \nlinear_changes
## 1398: 400 linear_changes 398 22 \nlinear_changes
## 1399: 400 linear_changes 399 21 \nlinear_changes
## 1400: 400 linear_changes 400 23 \nlinear_changes
library(ggplot2)
ggplot()+
theme_bw()+
theme(text=element_text(size=14))+
geom_vline(aes(
xintercept=end+0.5),
data=sim_changes)+
geom_point(aes(
data_index, data_value),
color="grey50",
data=sim_data)+
facet_grid(Simulation ~ N_data, labeller=label_both, scales="free_x", space="free")+
scale_x_continuous(
breaks=seq(0,max(N_data_vec),by=50))
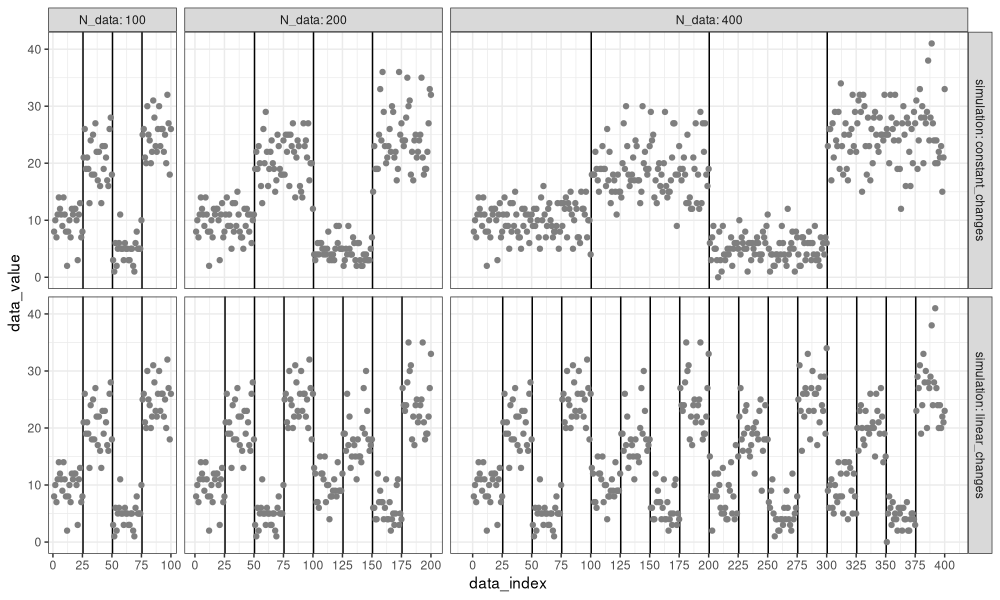
We see in the figure above that the data are the same in the two simulations, when there are only 100 data points. However, when there are 200 or 400 data, we see a difference:
- For the
constant_changessimulation, the number of change-points is still three (change-point every quarter of the data). - For the
linear_changessimulation, the number of change-points has increased from 3 to 7 to 15 (change-point every 25 data points).
PELT
Below we define a function which implements PELT for the Poisson loss, because we used a count data simulation above.
PELT <- function(sim.mat, penalty, prune=TRUE, verbose=FALSE){
if(!is.matrix(sim.mat))sim.mat <- cbind(sim.mat)
cum.data <- rbind(0, apply(sim.mat, 2, cumsum))
sum_trick <- function(m, start, end)m[end+1,,drop=FALSE]-m[start,,drop=FALSE]
cost_trick <- function(start, end){
sum_vec <- sum_trick(cum.data, start, end)
N <- end+1-start
mean_vec <- sum_vec/N
ifelse(sum_vec==0, 0, sum_vec*(1-log(mean_vec)))
}
N.data <- nrow(sim.mat)
pelt.change.vec <- rep(NA_integer_, N.data)
pelt.cost.vec <- rep(NA_real_, N.data+1)
pelt.cost.vec[1] <- -penalty
pelt.candidates.vec <- rep(NA_integer_, N.data)
candidate.vec <- 1L
if(verbose)index_dt_list <- list()
for(up.to in 1:N.data){
N.cand <- length(candidate.vec)
pelt.candidates.vec[up.to] <- N.cand
last.seg.cost <- rowSums(cost_trick(candidate.vec, rep(up.to, N.cand)))
prev.cost <- pelt.cost.vec[candidate.vec]
cost.no.penalty <- prev.cost+last.seg.cost
total.cost <- cost.no.penalty+penalty
if(verbose)index_dt_list[[up.to]] <- data.table(
data_index=up.to, change=candidate.vec, cost=total.cost/up.to)
best.i <- which.min(total.cost)
pelt.change.vec[up.to] <- candidate.vec[best.i]
total.cost.best <- total.cost[best.i]
pelt.cost.vec[up.to+1] <- total.cost.best
keep <- if(isTRUE(prune))cost.no.penalty < total.cost.best else TRUE
candidate.vec <- c(candidate.vec[keep], up.to+1L)
}
list(
change=pelt.change.vec,
cost=pelt.cost.vec,
candidates=pelt.candidates.vec,
index_dt=if(verbose)rbindlist(index_dt_list))
}
decode <- function(best.change){
seg.dt.list <- list()
last.i <- length(best.change)
while(last.i>0){
first.i <- best.change[last.i]
seg.dt.list[[paste(last.i)]] <- data.table(
first.i, last.i)
last.i <- first.i-1L
}
rbindlist(seg.dt.list)[seq(.N,1)]
}
pelt_info_list <- list()
pelt_segs_list <- list()
both_index_list <- list()
penalty <- 10
algo.prune <- c(
OPART=FALSE,
PELT=TRUE)
for(N_data in N_data_vec){
for(simulation in names(sim_fun_list)){
N_sim <- paste(N_data, simulation)
data_value <- sim_data_list[[N_sim]]$data_value
for(algo in names(algo.prune)){
prune <- algo.prune[[algo]]
fit <- PELT(data_value, penalty=penalty, prune=prune, verbose = TRUE)
both_index_list[[paste(N_data, simulation, algo)]] <- data.table(
N_data, simulation, algo, fit$index_dt)
fit_seg_dt <- decode(fit$change)
pelt_info_list[[paste(N_data,simulation,algo)]] <- data.table(
N_data,simulation,algo,
candidates=fit$candidates,data_index=seq_along(data_value))
pelt_segs_list[[paste(N_data,simulation,algo)]] <- data.table(
N_data,simulation,algo,
fit_seg_dt)
}
}
}
(pelt_info <- addSim(rbindlist(pelt_info_list)))
## N_data simulation algo candidates data_index Simulation
## <num> <char> <char> <int> <int> <char>
## 1: 100 constant_changes OPART 1 1 \nconstant_changes
## 2: 100 constant_changes OPART 2 2 \nconstant_changes
## 3: 100 constant_changes OPART 3 3 \nconstant_changes
## 4: 100 constant_changes OPART 4 4 \nconstant_changes
## 5: 100 constant_changes OPART 5 5 \nconstant_changes
## ---
## 2796: 400 linear_changes PELT 20 396 \nlinear_changes
## 2797: 400 linear_changes PELT 20 397 \nlinear_changes
## 2798: 400 linear_changes PELT 21 398 \nlinear_changes
## 2799: 400 linear_changes PELT 22 399 \nlinear_changes
## 2800: 400 linear_changes PELT 23 400 \nlinear_changes
(pelt_segs <- addSim(rbindlist(pelt_segs_list)))
## N_data simulation algo first.i last.i Simulation
## <num> <char> <char> <int> <int> <char>
## 1: 100 constant_changes OPART 1 25 \nconstant_changes
## 2: 100 constant_changes OPART 26 50 \nconstant_changes
## 3: 100 constant_changes OPART 51 75 \nconstant_changes
## 4: 100 constant_changes OPART 76 100 \nconstant_changes
## 5: 100 constant_changes PELT 1 25 \nconstant_changes
## 6: 100 constant_changes PELT 26 50 \nconstant_changes
## 7: 100 constant_changes PELT 51 75 \nconstant_changes
## 8: 100 constant_changes PELT 76 100 \nconstant_changes
## 9: 100 linear_changes OPART 1 25 \nlinear_changes
## 10: 100 linear_changes OPART 26 50 \nlinear_changes
## 11: 100 linear_changes OPART 51 75 \nlinear_changes
## 12: 100 linear_changes OPART 76 100 \nlinear_changes
## 13: 100 linear_changes PELT 1 25 \nlinear_changes
## 14: 100 linear_changes PELT 26 50 \nlinear_changes
## 15: 100 linear_changes PELT 51 75 \nlinear_changes
## 16: 100 linear_changes PELT 76 100 \nlinear_changes
## 17: 200 constant_changes OPART 1 50 \nconstant_changes
## 18: 200 constant_changes OPART 51 100 \nconstant_changes
## 19: 200 constant_changes OPART 101 150 \nconstant_changes
## 20: 200 constant_changes OPART 151 200 \nconstant_changes
## 21: 200 constant_changes PELT 1 50 \nconstant_changes
## 22: 200 constant_changes PELT 51 100 \nconstant_changes
## 23: 200 constant_changes PELT 101 150 \nconstant_changes
## 24: 200 constant_changes PELT 151 200 \nconstant_changes
## 25: 200 linear_changes OPART 1 25 \nlinear_changes
## 26: 200 linear_changes OPART 26 50 \nlinear_changes
## 27: 200 linear_changes OPART 51 75 \nlinear_changes
## 28: 200 linear_changes OPART 76 100 \nlinear_changes
## 29: 200 linear_changes OPART 101 125 \nlinear_changes
## 30: 200 linear_changes OPART 126 150 \nlinear_changes
## 31: 200 linear_changes OPART 151 175 \nlinear_changes
## 32: 200 linear_changes OPART 176 200 \nlinear_changes
## 33: 200 linear_changes PELT 1 25 \nlinear_changes
## 34: 200 linear_changes PELT 26 50 \nlinear_changes
## 35: 200 linear_changes PELT 51 75 \nlinear_changes
## 36: 200 linear_changes PELT 76 100 \nlinear_changes
## 37: 200 linear_changes PELT 101 125 \nlinear_changes
## 38: 200 linear_changes PELT 126 150 \nlinear_changes
## 39: 200 linear_changes PELT 151 175 \nlinear_changes
## 40: 200 linear_changes PELT 176 200 \nlinear_changes
## 41: 400 constant_changes OPART 1 100 \nconstant_changes
## 42: 400 constant_changes OPART 101 200 \nconstant_changes
## 43: 400 constant_changes OPART 201 300 \nconstant_changes
## 44: 400 constant_changes OPART 301 400 \nconstant_changes
## 45: 400 constant_changes PELT 1 100 \nconstant_changes
## 46: 400 constant_changes PELT 101 200 \nconstant_changes
## 47: 400 constant_changes PELT 201 300 \nconstant_changes
## 48: 400 constant_changes PELT 301 400 \nconstant_changes
## 49: 400 linear_changes OPART 1 25 \nlinear_changes
## 50: 400 linear_changes OPART 26 50 \nlinear_changes
## 51: 400 linear_changes OPART 51 75 \nlinear_changes
## 52: 400 linear_changes OPART 76 100 \nlinear_changes
## 53: 400 linear_changes OPART 101 125 \nlinear_changes
## 54: 400 linear_changes OPART 126 150 \nlinear_changes
## 55: 400 linear_changes OPART 151 175 \nlinear_changes
## 56: 400 linear_changes OPART 176 201 \nlinear_changes
## 57: 400 linear_changes OPART 202 224 \nlinear_changes
## 58: 400 linear_changes OPART 225 250 \nlinear_changes
## 59: 400 linear_changes OPART 251 275 \nlinear_changes
## 60: 400 linear_changes OPART 276 300 \nlinear_changes
## 61: 400 linear_changes OPART 301 325 \nlinear_changes
## 62: 400 linear_changes OPART 326 350 \nlinear_changes
## 63: 400 linear_changes OPART 351 375 \nlinear_changes
## 64: 400 linear_changes OPART 376 400 \nlinear_changes
## 65: 400 linear_changes PELT 1 25 \nlinear_changes
## 66: 400 linear_changes PELT 26 50 \nlinear_changes
## 67: 400 linear_changes PELT 51 75 \nlinear_changes
## 68: 400 linear_changes PELT 76 100 \nlinear_changes
## 69: 400 linear_changes PELT 101 125 \nlinear_changes
## 70: 400 linear_changes PELT 126 150 \nlinear_changes
## 71: 400 linear_changes PELT 151 175 \nlinear_changes
## 72: 400 linear_changes PELT 176 201 \nlinear_changes
## 73: 400 linear_changes PELT 202 224 \nlinear_changes
## 74: 400 linear_changes PELT 225 250 \nlinear_changes
## 75: 400 linear_changes PELT 251 275 \nlinear_changes
## 76: 400 linear_changes PELT 276 300 \nlinear_changes
## 77: 400 linear_changes PELT 301 325 \nlinear_changes
## 78: 400 linear_changes PELT 326 350 \nlinear_changes
## 79: 400 linear_changes PELT 351 375 \nlinear_changes
## 80: 400 linear_changes PELT 376 400 \nlinear_changes
## N_data simulation algo first.i last.i Simulation
We see in the result tables above that the segmentations are the same, using pruning and no pruning. Below we visualize the number of candidates considered.
algo.colors <- c(
OPART="grey50",
PELT="red",
DUST="deepskyblue",
FPOP="blue")
ggplot()+
theme_bw()+
theme(
panel.spacing=grid::unit(1,"lines"),
text=element_text(size=15))+
geom_vline(aes(
xintercept=end+0.5),
data=sim_changes)+
scale_color_manual(
breaks=names(algo.colors),
values=algo.colors)+
geom_point(aes(
data_index, candidates, color=algo),
data=pelt_info)+
facet_grid(Simulation ~ N_data, labeller=label_both, scales="free_x", space="free")+
scale_x_continuous(
breaks=seq(0,max(N_data_vec),by=50))
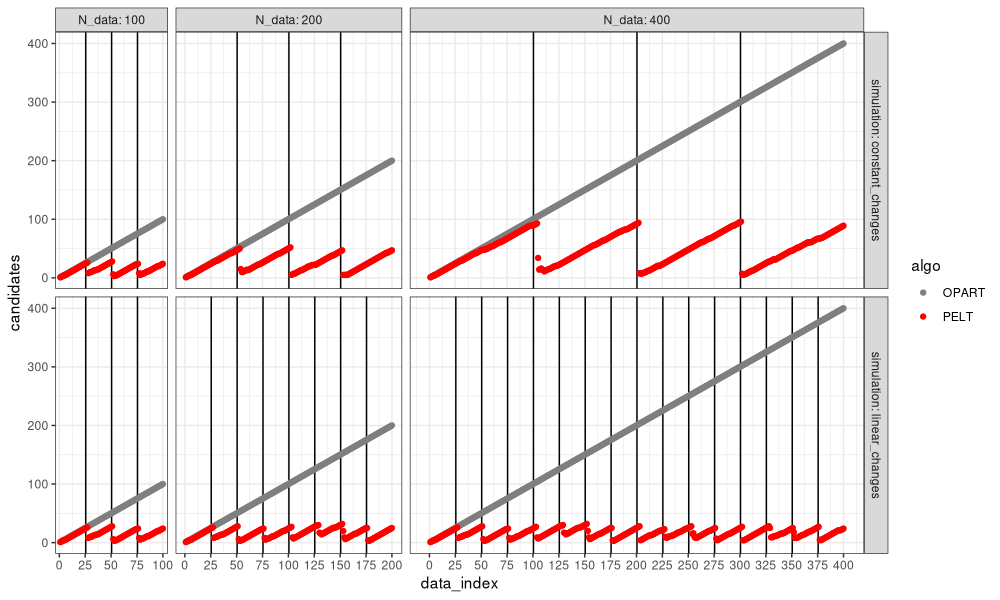
We can see in the figure above that PELT considers a much smaller number of change-points, that tends to reset near zero, for each change-point detected.
- In the bottom simulation with linear changes, the number of change-point candidates considered by PELT is constant (does not depend on number of data), so PELT is linear time, whereas OPART is quadratic, in the number of data.
- In the top simulation with constant changes, the number of change-point candidates considered by PELT is linear in the number of data, so both OPART and PELT are quadratic time in the number of data.
FPOP
Now we run FPOP, which is another pruning method, which is more complex to implement efficiently, so we use C++ code in the R package PeakSegOptimal.
if(FALSE){
remotes::install_github("tdhock/PeakSegOptimal@f05834ad4b452070da1818f25412e5ac97454833")
}
fpop_info_list <- list()
fpop_segs_list <- list()
for(N_data in N_data_vec){
for(simulation in names(sim_fun_list)){
N_sim <- paste(N_data, simulation)
data_value <- sim_data_list[[N_sim]]$data_value
pfit <- PeakSegOptimal::UnconstrainedFPOP(
data_value, penalty=penalty, verbose_file=tempfile())
both_index_list[[paste(N_data, simulation, "FPOP")]] <- unique(data.table(
N_data, simulation, algo="FPOP", pfit$index_dt
)[, let(
data_index=data_index+1L,
change=change+2L
)])
start <- rev(with(pfit, ends.vec[ends.vec>=0])+1L)
end <- c(start[-1]-1L,length(data_value))
fpop_info_list[[paste(N_data,simulation)]] <- data.table(
N_data,simulation,
algo="FPOP",
candidates=pfit$intervals.vec,
data_index=seq_along(data_value))
fpop_segs_list[[paste(N_data,simulation)]] <- data.table(
N_data,simulation,start,end)
}
}
(fpop_info <- addSim(rbindlist(fpop_info_list)))
## N_data simulation algo candidates data_index Simulation
## <num> <char> <char> <int> <int> <char>
## 1: 100 constant_changes FPOP 1 1 \nconstant_changes
## 2: 100 constant_changes FPOP 2 2 \nconstant_changes
## 3: 100 constant_changes FPOP 3 3 \nconstant_changes
## 4: 100 constant_changes FPOP 3 4 \nconstant_changes
## 5: 100 constant_changes FPOP 3 5 \nconstant_changes
## ---
## 1396: 400 linear_changes FPOP 5 396 \nlinear_changes
## 1397: 400 linear_changes FPOP 5 397 \nlinear_changes
## 1398: 400 linear_changes FPOP 6 398 \nlinear_changes
## 1399: 400 linear_changes FPOP 6 399 \nlinear_changes
## 1400: 400 linear_changes FPOP 6 400 \nlinear_changes
(fpop_segs <- rbindlist(fpop_segs_list))
## N_data simulation start end
## <num> <char> <int> <int>
## 1: 100 constant_changes 26 50
## 2: 100 constant_changes 51 75
## 3: 100 constant_changes 76 100
## 4: 100 constant_changes 101 100
## 5: 100 linear_changes 26 50
## 6: 100 linear_changes 51 75
## 7: 100 linear_changes 76 100
## 8: 100 linear_changes 101 100
## 9: 200 constant_changes 51 100
## 10: 200 constant_changes 101 150
## 11: 200 constant_changes 151 200
## 12: 200 constant_changes 201 200
## 13: 200 linear_changes 26 50
## 14: 200 linear_changes 51 75
## 15: 200 linear_changes 76 100
## 16: 200 linear_changes 101 125
## 17: 200 linear_changes 126 150
## 18: 200 linear_changes 151 175
## 19: 200 linear_changes 176 200
## 20: 200 linear_changes 201 200
## 21: 400 constant_changes 101 200
## 22: 400 constant_changes 201 300
## 23: 400 constant_changes 301 400
## 24: 400 constant_changes 401 400
## 25: 400 linear_changes 26 50
## 26: 400 linear_changes 51 75
## 27: 400 linear_changes 76 100
## 28: 400 linear_changes 101 125
## 29: 400 linear_changes 126 150
## 30: 400 linear_changes 151 175
## 31: 400 linear_changes 176 201
## 32: 400 linear_changes 202 224
## 33: 400 linear_changes 225 250
## 34: 400 linear_changes 251 275
## 35: 400 linear_changes 276 300
## 36: 400 linear_changes 301 325
## 37: 400 linear_changes 326 350
## 38: 400 linear_changes 351 375
## 39: 400 linear_changes 376 400
## 40: 400 linear_changes 401 400
## N_data simulation start end
both_info <- rbind(pelt_info, fpop_info)
ggplot()+
theme_bw()+
theme(
panel.spacing=grid::unit(1,"lines"),
text=element_text(size=15))+
geom_vline(aes(
xintercept=end+0.5),
data=sim_changes)+
scale_color_manual(
breaks=names(algo.colors),
values=algo.colors)+
geom_point(aes(
data_index, candidates, color=algo),
data=both_info)+
facet_grid(Simulation ~ N_data, labeller=label_both, scales="free_x", space="free")+
scale_x_continuous(
breaks=seq(0,max(N_data_vec),by=50))
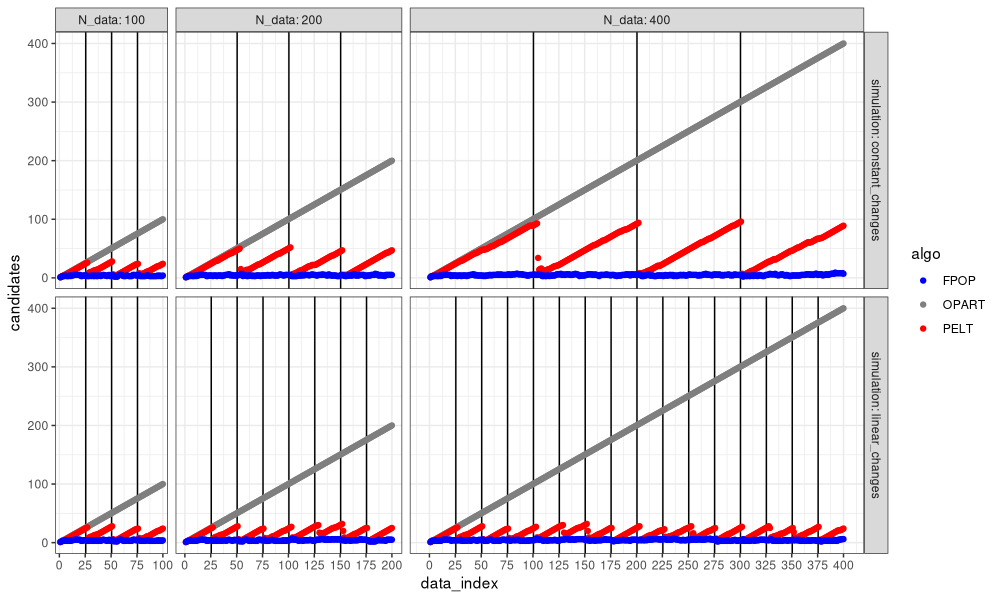
In the figure above, we can see the advantage of FPOP: the number of change-points considered does not increase with the number of data, even with constant number of changes (larger segments).
- In the top simulation with constant changes, the number of change-points candidates considered is linear in the number of data, so both OPART and PELT are quadratic time in the number of data, whereas FPOP is sub-quadratic (empirically linear or log-linear).
DuST
DuST is a new pruning technique based on Lagrange duality, proposed by Truong and Runge, Stat, 2024.
if(FALSE){
remotes::install_github("vrunge/dust@910f8c67f99354fdb5ff7740e6436eb487d9efa6")
}
set.seed(1)
ex_data <- rpois(7,100)
ex_penalty <- 1
dfit <- dust::dust.1D(ex_data,ex_penalty,"poisson")
rbind(
PELT=PELT(ex_data,ex_penalty)$cost[-1]/seq_along(ex_data),
FPOP=PeakSegOptimal::UnconstrainedFPOP(ex_data,penalty=ex_penalty)$cost,
DUST=dfit$costQ/seq_along(ex_data))
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## PELT -328.5318 -374.3771 -388.3987 -385.9978 -366.236 -368.2061 -371.7383
## FPOP -328.5318 -374.3771 -388.3987 -385.9978 -366.236 -368.2061 -371.7383
## DUST -328.5318 -374.3771 -388.3987 -385.9978 -366.236 -368.2061 -371.7383
The code above verifies that we compute the cost in the same way for each algorithm. In particular, PELT and DUST return the total cost, so we need to divide by the number of data points to get the average cost, which is returned by FPOP. Below we compute the candidates considered by DUST, for each of the two simulations, and a variety of data sizes.
dust_info_list <- list()
dust_segs_list <- list()
for(N_data in N_data_vec){
for(simulation in names(sim_fun_list)){
N_sim <- paste(N_data, simulation)
data_value <- sim_data_list[[N_sim]]$data_value
dfit <- dust::dust.object.1D("poisson")
candidates <- rep(NA_integer_, N_data)
for(data_index in seq_along(data_value)){
dfit$append_c(data_value[[data_index]], penalty)
dfit$update_partition()
pinfo <- dfit$get_partition()
change <- pinfo$lastIndexSet[-1]+1L
candidates[[data_index]] <- length(change)
mean_cost <- pinfo$costQ/seq_along(pinfo$costQ)
both_index_list[[paste(
N_data, simulation, "DUST", data_index
)]] <- data.table(
N_data, simulation, algo="DUST", data_index,
change, cost=mean_cost[change])
}
end <- pinfo$changepoints
start <- c(1, end[-length(end)]+1)
dust_info_list[[paste(N_data,simulation)]] <- data.table(
N_data,simulation,
algo="DUST",
candidates,
data_index=seq_along(data_value))
dust_segs_list[[paste(N_data,simulation)]] <- data.table(
N_data,simulation,start,end)
}
}
(dust_info <- addSim(rbindlist(dust_info_list)))
## N_data simulation algo candidates data_index Simulation
## <num> <char> <char> <int> <int> <char>
## 1: 100 constant_changes DUST 1 1 \nconstant_changes
## 2: 100 constant_changes DUST 1 2 \nconstant_changes
## 3: 100 constant_changes DUST 1 3 \nconstant_changes
## 4: 100 constant_changes DUST 1 4 \nconstant_changes
## 5: 100 constant_changes DUST 2 5 \nconstant_changes
## ---
## 1396: 400 linear_changes DUST 4 396 \nlinear_changes
## 1397: 400 linear_changes DUST 5 397 \nlinear_changes
## 1398: 400 linear_changes DUST 5 398 \nlinear_changes
## 1399: 400 linear_changes DUST 5 399 \nlinear_changes
## 1400: 400 linear_changes DUST 5 400 \nlinear_changes
(dust_segs <- rbindlist(dust_segs_list))
## N_data simulation start end
## <num> <char> <num> <num>
## 1: 100 constant_changes 1 25
## 2: 100 constant_changes 26 50
## 3: 100 constant_changes 51 75
## 4: 100 constant_changes 76 100
## 5: 100 linear_changes 1 25
## 6: 100 linear_changes 26 50
## 7: 100 linear_changes 51 75
## 8: 100 linear_changes 76 100
## 9: 200 constant_changes 1 50
## 10: 200 constant_changes 51 100
## 11: 200 constant_changes 101 150
## 12: 200 constant_changes 151 200
## 13: 200 linear_changes 1 25
## 14: 200 linear_changes 26 50
## 15: 200 linear_changes 51 75
## 16: 200 linear_changes 76 100
## 17: 200 linear_changes 101 125
## 18: 200 linear_changes 126 150
## 19: 200 linear_changes 151 175
## 20: 200 linear_changes 176 200
## 21: 400 constant_changes 1 100
## 22: 400 constant_changes 101 200
## 23: 400 constant_changes 201 300
## 24: 400 constant_changes 301 400
## 25: 400 linear_changes 1 25
## 26: 400 linear_changes 26 50
## 27: 400 linear_changes 51 75
## 28: 400 linear_changes 76 100
## 29: 400 linear_changes 101 125
## 30: 400 linear_changes 126 150
## 31: 400 linear_changes 151 175
## 32: 400 linear_changes 176 201
## 33: 400 linear_changes 202 224
## 34: 400 linear_changes 225 250
## 35: 400 linear_changes 251 275
## 36: 400 linear_changes 276 300
## 37: 400 linear_changes 301 325
## 38: 400 linear_changes 326 350
## 39: 400 linear_changes 351 375
## 40: 400 linear_changes 376 400
## N_data simulation start end
three_info <- rbind(pelt_info, fpop_info, dust_info)
ggplot()+
theme_bw()+
theme(
panel.spacing=grid::unit(1,"lines"),
text=element_text(size=15))+
geom_vline(aes(
xintercept=end+0.5),
data=sim_changes)+
scale_color_manual(
breaks=names(algo.colors),
values=algo.colors)+
geom_point(aes(
data_index, candidates, color=algo),
data=three_info)+
facet_grid(Simulation ~ N_data, labeller=label_both, scales="free_x", space="free")+
scale_x_continuous(
breaks=seq(0,max(N_data_vec),by=50))
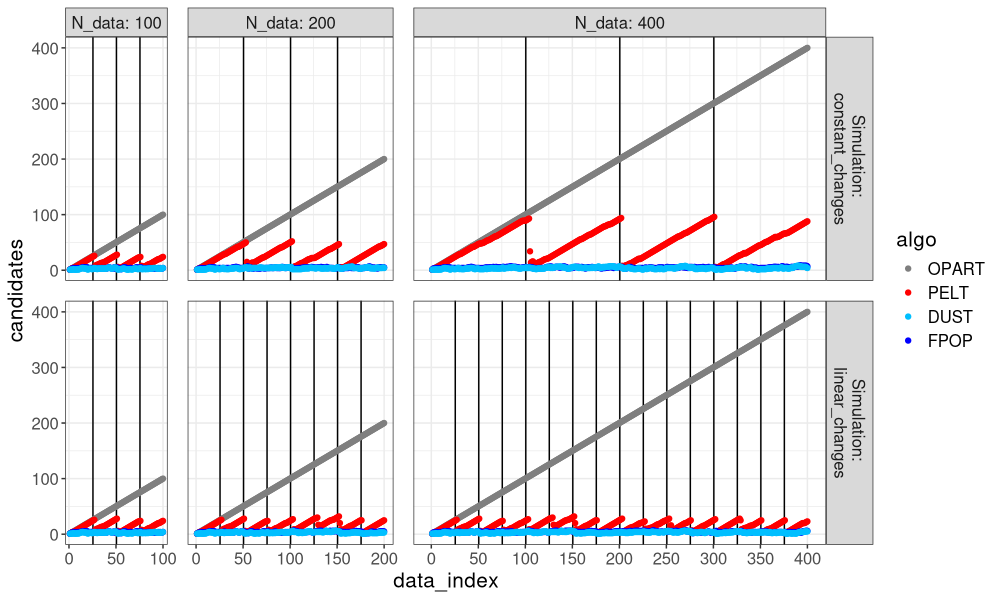
The figure above shows that DUST pruned much more than PELT, nearly the same amount as FPOP.
Heat maps
Another way to view this is by looking at the cost of each candidate change-point considered, as in the heat map below.
algo.levs <- c("OPART","PELT","FPOP")
algo.levs <- names(algo.colors)
(both_index <- addSim(rbindlist(both_index_list))[, let(
Algorithm = factor(algo, algo.levs)
)][])
## N_data simulation algo data_index change cost Simulation Algorithm
## <num> <char> <char> <int> <num> <num> <char> <fctr>
## 1: 100 constant_changes OPART 1 1 -8.635532 \nconstant_changes OPART
## 2: 100 constant_changes OPART 2 1 -10.775021 \nconstant_changes OPART
## 3: 100 constant_changes OPART 2 2 -5.830692 \nconstant_changes OPART
## 4: 100 constant_changes OPART 3 1 -9.335529 \nconstant_changes OPART
## 5: 100 constant_changes OPART 3 2 -6.005552 \nconstant_changes OPART
## ---
## 257086: 400 linear_changes DUST 400 397 -26.828554 \nlinear_changes DUST
## 257087: 400 linear_changes DUST 400 395 -26.734206 \nlinear_changes DUST
## 257088: 400 linear_changes DUST 400 394 -26.703759 \nlinear_changes DUST
## 257089: 400 linear_changes DUST 400 393 -26.639462 \nlinear_changes DUST
## 257090: 400 linear_changes DUST 400 376 -24.830653 \nlinear_changes DUST
both_index[data_index==2 & N_data==400 & simulation=="constant_changes"]
## N_data simulation algo data_index change cost Simulation Algorithm
## <num> <char> <char> <int> <num> <num> <char> <fctr>
## 1: 400 constant_changes OPART 2 1 -10.775021 \nconstant_changes OPART
## 2: 400 constant_changes OPART 2 2 -5.830692 \nconstant_changes OPART
## 3: 400 constant_changes PELT 2 1 -10.775021 \nconstant_changes PELT
## 4: 400 constant_changes PELT 2 2 -5.830692 \nconstant_changes PELT
## 5: 400 constant_changes FPOP 2 2 -5.830690 \nconstant_changes FPOP
## 6: 400 constant_changes FPOP 2 1 -10.775000 \nconstant_changes FPOP
## 7: 400 constant_changes DUST 2 1 -8.635532 \nconstant_changes DUST
for(a in algo.levs){
gg <- ggplot()+
ggtitle(a)+
theme_bw()+
theme(text=element_text(size=20))+
coord_equal()+
geom_tile(aes(
data_index, change, fill=cost),
data=both_index[Algorithm==a])+
scale_fill_gradient(low="black", high="red")+
facet_grid(Simulation ~ N_data, label=label_both)
print(gg)
}
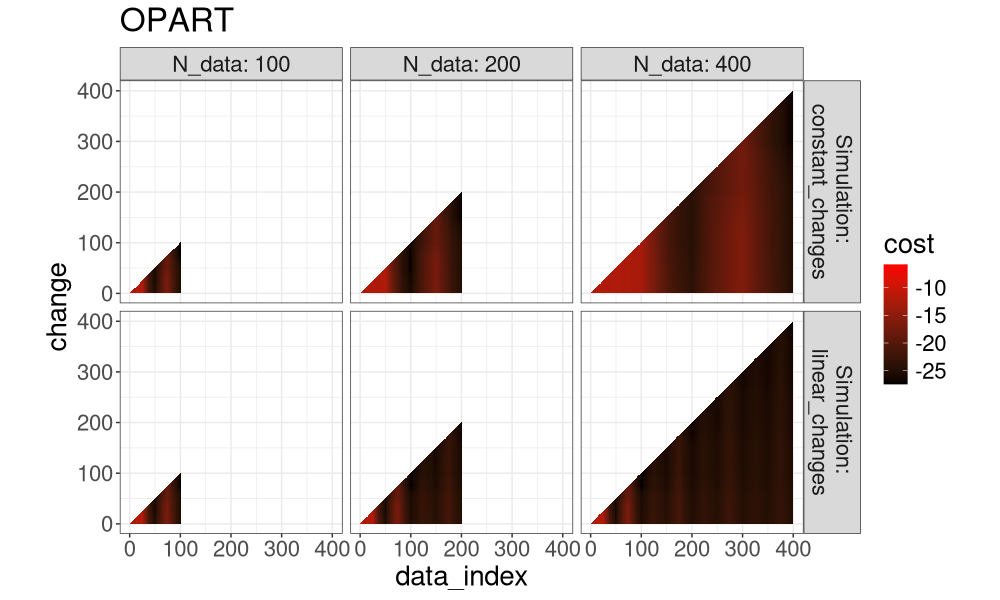
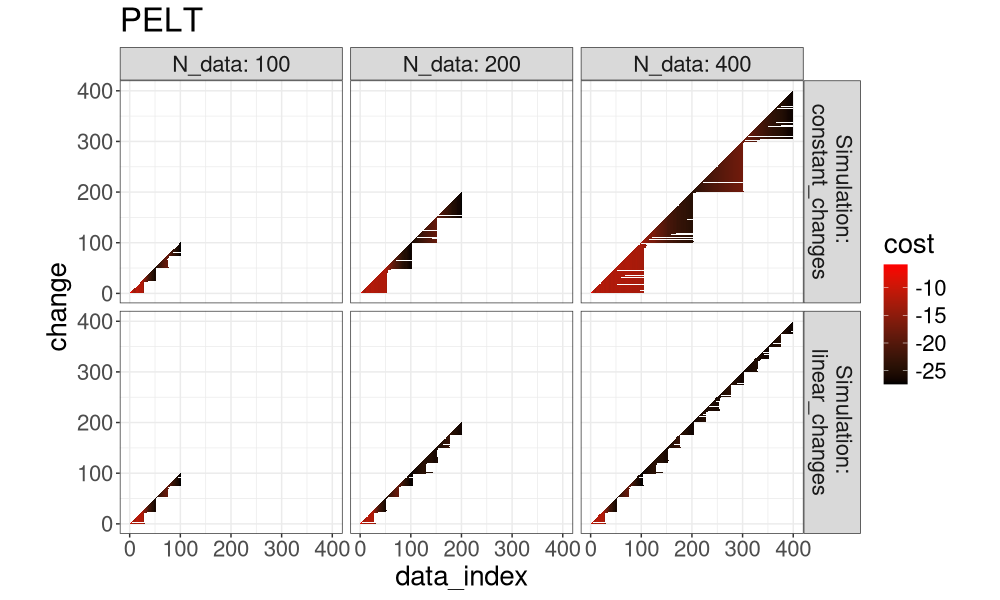
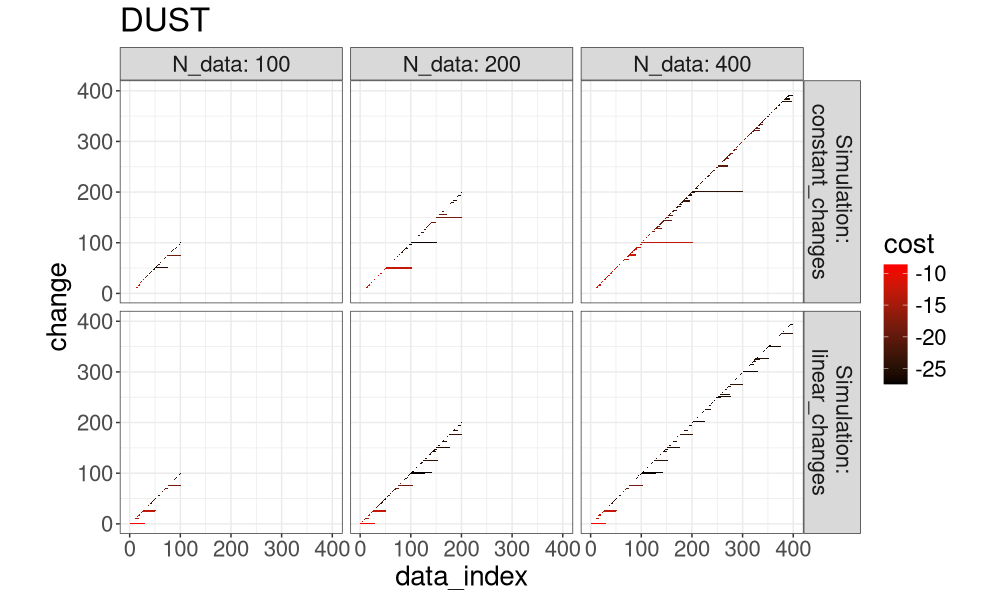
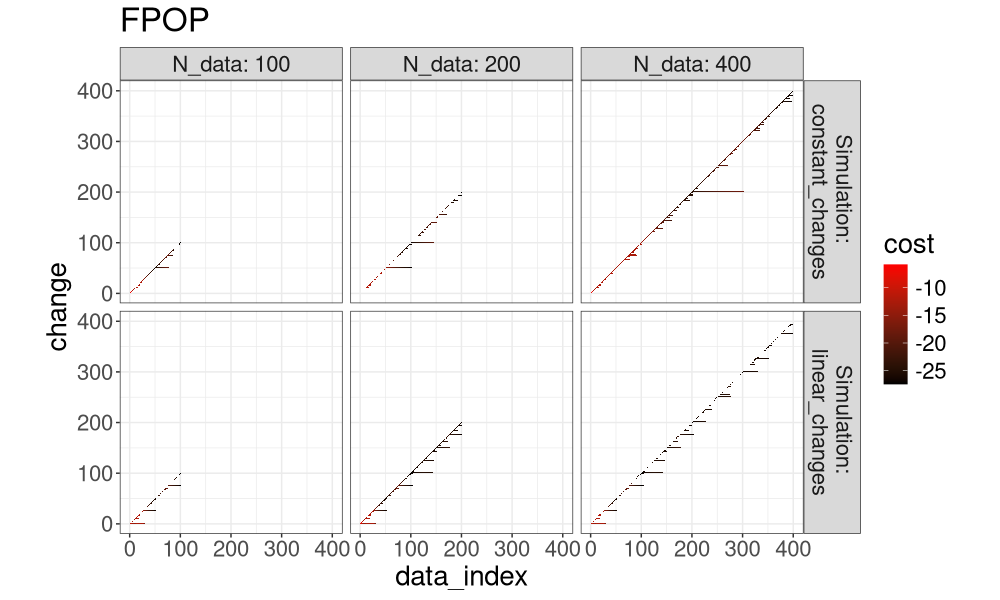
Another way to visualize it is in the plot below, which super-imposes the three algos.
ggplot()+
theme_bw()+
theme(text=element_text(size=15))+
geom_tile(aes(
data_index, change, fill=Algorithm),
data=both_index)+
scale_fill_manual(values=algo.colors)+
scale_x_continuous(
breaks=seq(0,max(N_data_vec),by=50))+
facet_grid(Simulation ~ N_data, label=label_both, scales="free", space="free")
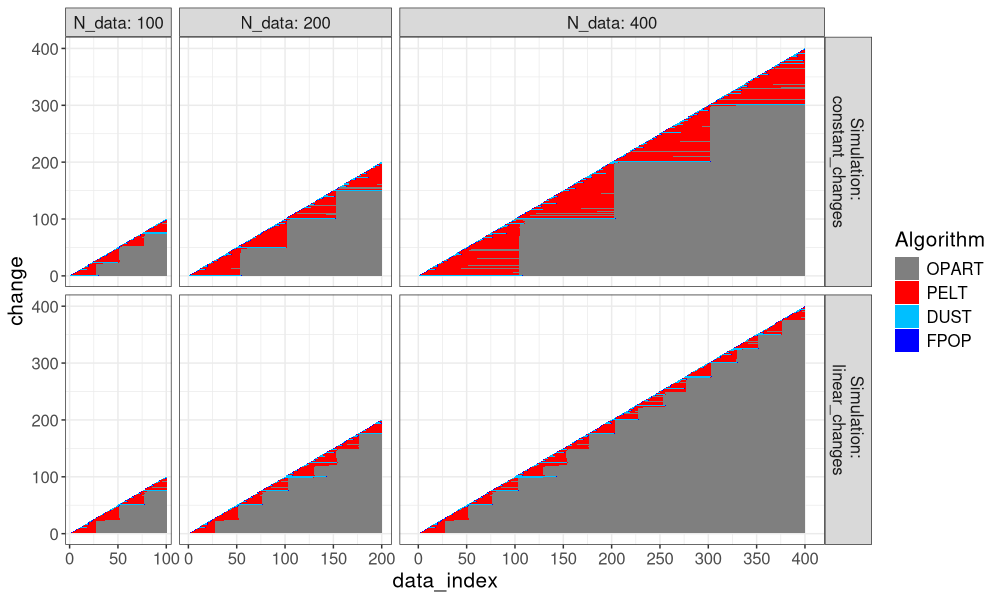
It is clear that FPOP prunes much more than PELT, especially in the case of constant changes (segments that get larger with the overall number of data). It is also clear that DUST considers nearly the same change-points as FPOP.
atime comparison
The atime() function can be used to perform asymptotic time/memory/etc comparisons.
This means that we will increase N, and monitor how fast certain quantities grow with N.
We begin by defining the data sizes N of interest:
base_N <- c(100,200,400,800)
(all_N <- unlist(lapply(10^seq(0,4), function(x)x*base_N)))
## [1] 1e+02 2e+02 4e+02 8e+02 1e+03 2e+03 4e+03 8e+03 1e+04 2e+04 4e+04 8e+04 1e+05 2e+05 4e+05 8e+05 1e+06 2e+06 4e+06
## [20] 8e+06
The data sizes above are on a log scale between 10 and 1,000,000. Next, we define a list that enumerates the different combinations in the experiment.
grid_args <- list(
list(simulation=names(sim_fun_list)),
DUST=quote({
dfit <- dust::dust.1D(data_list[[simulation]], penalty, "poisson")
with(dfit, data.frame(
mean_candidates=mean(nb),
segments=length(changepoints),
max_seg_size=max(diff(c(0,changepoints)))))
}),
FPOP=quote({
pfit <- PeakSegOptimal::UnconstrainedFPOP(
data_list[[simulation]], penalty=penalty)
data.frame(
mean_candidates=mean(pfit$intervals.vec),
segments=sum(is.finite(pfit$mean.vec)),
max_seg_size=max(-diff(pfit$ends.vec)))
}))
for(algo in names(algo.prune)){
prune <- algo.prune[[algo]]
grid_args[[algo]] <- substitute({
fit <- PELT(data_list[[simulation]], penalty=penalty, prune=prune)
dec <- decode(fit$change)
data.frame(
mean_candidates=mean(fit$candidates),
segments=nrow(dec),
max_seg_size=max(diff(c(0,dec$last.i))))
}, list(prune=prune))
}
(expr.list <- do.call(atime::atime_grid, grid_args))
## $`DUST simulation=constant_changes`
## {
## dfit <- dust::dust.1D(data_list[["constant_changes"]], penalty,
## "poisson")
## with(dfit, data.frame(mean_candidates = mean(nb), segments = length(changepoints),
## max_seg_size = max(diff(c(0, changepoints)))))
## }
##
## $`DUST simulation=linear_changes`
## {
## dfit <- dust::dust.1D(data_list[["linear_changes"]], penalty,
## "poisson")
## with(dfit, data.frame(mean_candidates = mean(nb), segments = length(changepoints),
## max_seg_size = max(diff(c(0, changepoints)))))
## }
##
## $`FPOP simulation=constant_changes`
## {
## pfit <- PeakSegOptimal::UnconstrainedFPOP(data_list[["constant_changes"]],
## penalty = penalty)
## data.frame(mean_candidates = mean(pfit$intervals.vec), segments = sum(is.finite(pfit$mean.vec)),
## max_seg_size = max(-diff(pfit$ends.vec)))
## }
##
## $`FPOP simulation=linear_changes`
## {
## pfit <- PeakSegOptimal::UnconstrainedFPOP(data_list[["linear_changes"]],
## penalty = penalty)
## data.frame(mean_candidates = mean(pfit$intervals.vec), segments = sum(is.finite(pfit$mean.vec)),
## max_seg_size = max(-diff(pfit$ends.vec)))
## }
##
## $`OPART simulation=constant_changes`
## {
## fit <- PELT(data_list[["constant_changes"]], penalty = penalty,
## prune = FALSE)
## dec <- decode(fit$change)
## data.frame(mean_candidates = mean(fit$candidates), segments = nrow(dec),
## max_seg_size = max(diff(c(0, dec$last.i))))
## }
##
## $`OPART simulation=linear_changes`
## {
## fit <- PELT(data_list[["linear_changes"]], penalty = penalty,
## prune = FALSE)
## dec <- decode(fit$change)
## data.frame(mean_candidates = mean(fit$candidates), segments = nrow(dec),
## max_seg_size = max(diff(c(0, dec$last.i))))
## }
##
## $`PELT simulation=constant_changes`
## {
## fit <- PELT(data_list[["constant_changes"]], penalty = penalty,
## prune = TRUE)
## dec <- decode(fit$change)
## data.frame(mean_candidates = mean(fit$candidates), segments = nrow(dec),
## max_seg_size = max(diff(c(0, dec$last.i))))
## }
##
## $`PELT simulation=linear_changes`
## {
## fit <- PELT(data_list[["linear_changes"]], penalty = penalty,
## prune = TRUE)
## dec <- decode(fit$change)
## data.frame(mean_candidates = mean(fit$candidates), segments = nrow(dec),
## max_seg_size = max(diff(c(0, dec$last.i))))
## }
##
## attr(,"parameters")
## expr.name expr.grid simulation
## <char> <char> <char>
## 1: DUST simulation=constant_changes DUST constant_changes
## 2: DUST simulation=linear_changes DUST linear_changes
## 3: FPOP simulation=constant_changes FPOP constant_changes
## 4: FPOP simulation=linear_changes FPOP linear_changes
## 5: OPART simulation=constant_changes OPART constant_changes
## 6: OPART simulation=linear_changes OPART linear_changes
## 7: PELT simulation=constant_changes PELT constant_changes
## 8: PELT simulation=linear_changes PELT linear_changes
Above we see a list with 8 expressions to run, and a data table with the corresponding number of rows. Note that each expression
- returns a data frame with one row and three columns that will be used as units to analyze as a function of N.
- should depend on data size N, which does not appear in the
expressions above, but it is used to define
data_listin thesetupargument below:
cache.rds <- "2025-02-25-PELT-vs-FPOP.rds"
if(file.exists(cache.rds)){
atime_list <- readRDS(cache.rds)
}else{
atime_list <- atime::atime(
N=all_N,
setup={
data_list <- list()
for(simulation in names(sim_fun_list)){
sim_fun <- sim_fun_list[[simulation]]
data_mean_vec <- sim_fun(N)
set.seed(1)
data_list[[simulation]] <- rpois(N, data_mean_vec)
}
},
expr.list=expr.list,
seconds.limit=1,
result=TRUE)
saveRDS(atime_list, cache.rds)
}
Note in the code above that we run the timing inside if(file.exists, which is a caching mechanism.
The result is time-consuming to compute, so the first time it is computed, it is saved to disk as an RDS file, and then subsequently read from disk, to save time.
Finally, we plot the different units as a function of data size N, in the figure below.
refs_list <- atime::references_best(atime_list)
ggplot()+
theme(
axis.text.x=element_text(size=12,angle=30,hjust=1),
text=element_text(size=12))+
directlabels::geom_dl(aes(
N, empirical, color=expr.grid, label=expr.grid),
data=refs_list$measurements,
method="right.polygons")+
geom_line(aes(
N, empirical, color=expr.grid),
data=refs_list$measurements)+
scale_color_manual(
"algorithm",
guide="none",
values=algo.colors)+
facet_grid(unit ~ simulation, scales="free")+
scale_x_log10(
"N = number of data in sequence",
breaks=10^seq(2,7),
limits=c(NA, 1e8))+
scale_y_log10("")
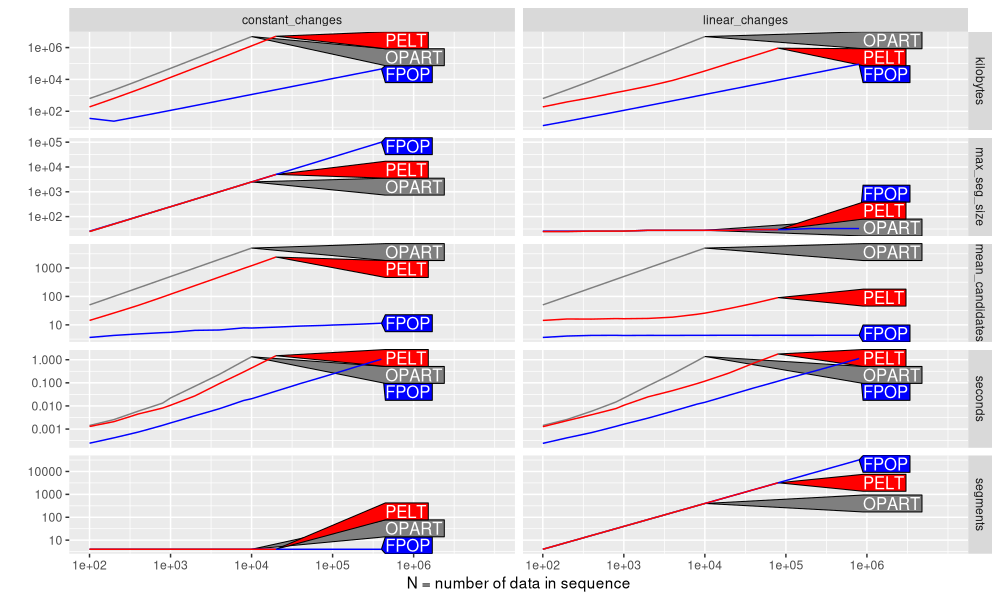
Above the figure shows a different curve for each algorithm, and a different panel for each simulation and measurement unit. We can observe that
- PELT memory usage in kilobytes has a larger slope for constant changes, than for linear changes. This implies a larger asymptotic complexity class.
- The maximum segment size,
max_seg_size, is the same for all algos, indicating that the penalty was chosen appropriately, and the algorithms are computing the same optimal solution. - Similarly, the mean number of candidates considered by the PELT algorithm has a larger slope for constant changes (same as OPART/linear in N), than for linear changes (relatively constant).
- For PELT seconds, we see a slightly larger slope for seconds in constant changes, compared to linear changes.
- As expected, number of
segmentsis constant for a constant number of changes (left), and increasing for a linear number of changes (right).
Below we plot the same data in a different way, that facilitates comparisons across the type of simulation:
refs_list$meas[, let(
Simulation = sub("_","\n",simulation),
Algorithm = factor(expr.grid, algo.levs)
)][]
## unit expr.name fun.name fun.latex expr.grid simulation N min
## <char> <char> <char> <char> <char> <char> <num> <num>
## 1: kilobytes DUST simulation=constant_changes N N DUST constant_changes 1e+02 0.0003783300
## 2: kilobytes DUST simulation=linear_changes N N DUST linear_changes 1e+02 0.0003679921
## 3: kilobytes FPOP simulation=constant_changes N N FPOP constant_changes 1e+02 0.0002385300
## 4: kilobytes FPOP simulation=linear_changes N N FPOP linear_changes 1e+02 0.0002388670
## 5: kilobytes OPART simulation=constant_changes N^2 N^2 OPART constant_changes 1e+02 0.0017725271
## ---
## 531: max_seg_size DUST simulation=linear_changes <NA> <NA> DUST linear_changes 1e+06 0.2073926179
## 532: max_seg_size DUST simulation=constant_changes N N DUST constant_changes 2e+06 1.2038735760
## 533: max_seg_size DUST simulation=linear_changes <NA> <NA> DUST linear_changes 2e+06 0.4109501251
## 534: max_seg_size DUST simulation=linear_changes <NA> <NA> DUST linear_changes 4e+06 0.8158070830
## 535: max_seg_size DUST simulation=linear_changes <NA> <NA> DUST linear_changes 8e+06 1.7653503710
## median itr/sec gc/sec n_itr n_gc result time
## <num> <num> <num> <int> <num> <list> <list>
## 1: 0.0004352505 2154.4517374 0.0000000 10 0 <data.frame[1x3]> 684µs,461µs,559µs,460µs,443µs,428µs,...
## 2: 0.0004020535 2401.6036997 0.0000000 10 0 <data.frame[1x3]> 539µs,440µs,376µs,375µs,368µs,368µs,...
## 3: 0.0002547929 3821.8312727 0.0000000 10 0 <data.frame[1x3]> 352µs,266µs,253µs,257µs,244µs,239µs,...
## 4: 0.0002549275 3717.6576328 0.0000000 10 0 <data.frame[1x3]> 330µs,259µs,245µs,251µs,244µs,260µs,...
## 5: 0.0018963466 512.9685126 0.0000000 10 0 <data.frame[1x3]> 2.22ms,1.95ms,1.9ms,2.25ms,1.88ms,1.8ms,...
## ---
## 531: 0.2092330895 4.7958287 2.0553552 7 3 <data.frame[1x3]> 215ms,207ms,208ms,208ms,211ms,210ms,...
## 532: 1.2085569665 0.8285637 0.5523758 6 4 <data.frame[1x3]> 1.21s,1.2s,1.21s,1.21s,1.22s,1.21s,...
## 533: 0.4198099815 2.3654731 2.8385677 5 6 <data.frame[1x3]> 411ms,421ms,412ms,413ms,413ms,428ms,...
## 534: 0.8427591324 1.1720689 5.8603445 2 10 <data.frame[1x3]> 891ms,908ms,944ms,816ms,842ms,835ms,...
## 535: 1.8154073436 0.5504069 1.0457731 10 19 <data.frame[1x3]> 1.85s,1.77s,1.88s,1.77s,1.77s,1.76s,...
## gc kilobytes q25 q75 max mean sd mean_candidates
## <list> <num> <num> <num> <num> <num> <num> <num>
## 1: <tbl_df[10x3]> 2.771094e+01 0.0004209292 0.0004610748 0.0006840620 0.0004641552 9.201532e-05 2.670000
## 2: <tbl_df[10x3]> 4.414062e+00 0.0003704191 0.0004380470 0.0005388900 0.0004163884 5.674954e-05 2.670000
## 3: <tbl_df[10x3]> 1.260156e+01 0.0002417532 0.0002634847 0.0003524380 0.0002616547 3.369264e-05 3.620000
## 4: <tbl_df[10x3]> 1.260156e+01 0.0002441385 0.0002641595 0.0003569479 0.0002689866 4.085838e-05 3.620000
## 5: <tbl_df[10x3]> 8.858906e+02 0.0018204999 0.0020173791 0.0022495311 0.0019494374 1.699584e-04 50.500000
## ---
## 531: <tbl_df[10x3]> 4.156473e+04 0.2079193987 0.2104281450 0.2152205879 0.2098437335 2.562125e-03 3.217038
## 532: <tbl_df[10x3]> 7.812627e+04 1.2058141263 1.2152456919 1.2191310481 1.2103568259 5.685315e-03 17.992054
## 533: <tbl_df[10x3]> 8.312638e+04 0.4129259010 0.4416093705 0.4589046910 0.4271669130 1.776231e-02 3.215730
## 534: <tbl_df[10x3]> 1.662524e+05 0.8338015667 0.8974753255 0.9439399519 0.8642597747 4.272027e-02 3.213032
## 535: <tbl_df[10x3]> 3.325031e+05 1.7716509304 1.8610300747 1.8748299400 1.8168377176 4.841334e-02 3.212893
## segments max_seg_size expr.class expr.latex
## <int> <num> <char> <char>
## 1: 4 25 DUST simulation=constant_changes\nN DUST simulation=constant_changes\n$O(N)$
## 2: 4 25 DUST simulation=linear_changes\nN DUST simulation=linear_changes\n$O(N)$
## 3: 4 26 FPOP simulation=constant_changes\nN FPOP simulation=constant_changes\n$O(N)$
## 4: 4 26 FPOP simulation=linear_changes\nN FPOP simulation=linear_changes\n$O(N)$
## 5: 4 25 OPART simulation=constant_changes\nN^2 OPART simulation=constant_changes\n$O(N^2)$
## ---
## 531: 40003 33 DUST simulation=linear_changes\nNA DUST simulation=linear_changes\n$O(NA)$
## 532: 4 500000 DUST simulation=constant_changes\nN DUST simulation=constant_changes\n$O(N)$
## 533: 80005 34 DUST simulation=linear_changes\nNA DUST simulation=linear_changes\n$O(NA)$
## 534: 160014 34 DUST simulation=linear_changes\nNA DUST simulation=linear_changes\n$O(NA)$
## 535: 320033 38 DUST simulation=linear_changes\nNA DUST simulation=linear_changes\n$O(NA)$
## empirical Simulation Algorithm
## <num> <char> <fctr>
## 1: 2.771094e+01 constant\nchanges DUST
## 2: 4.414062e+00 linear\nchanges DUST
## 3: 1.260156e+01 constant\nchanges FPOP
## 4: 1.260156e+01 linear\nchanges FPOP
## 5: 8.858906e+02 constant\nchanges OPART
## ---
## 531: 3.300000e+01 linear\nchanges DUST
## 532: 5.000000e+05 constant\nchanges DUST
## 533: 3.400000e+01 linear\nchanges DUST
## 534: 3.400000e+01 linear\nchanges DUST
## 535: 3.800000e+01 linear\nchanges DUST
ggplot()+
theme(
axis.text.x=element_text(size=12,angle=30,hjust=1),
legend.position="none",
text=element_text(size=12))+
directlabels::geom_dl(aes(
N, empirical, color=Simulation, label=Simulation),
data=refs_list$measurements,
method="right.polygons")+
geom_line(aes(
N, empirical, color=Simulation),
data=refs_list$measurements)+
facet_grid(unit ~ Algorithm, scales="free")+
scale_x_log10(
"N = number of data in sequence",
breaks=10^seq(2,7),
limits=c(NA, 1e8))+
scale_y_log10("")
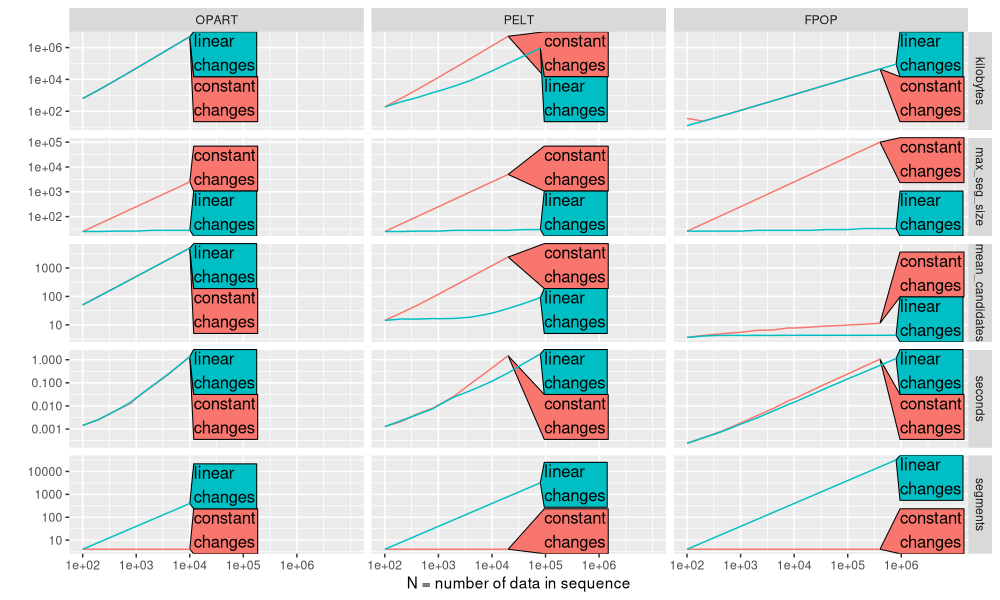
The plot above makes it easier to notice some interesting trends in the mean number of candidates:
- For PELT and FPOP the mean number of candidates is increases for a constant number of changes, but at different rates (FPOP much slower than PELT).
expr.levs <- CJ(
algo=algo.levs,
simulation=names(sim_fun_list)
)[algo.levs, paste0(algo,"\n",simulation), on="algo"]
edit_expr <- function(DT)DT[
, expr.name := factor(sub(" simulation=", "\n", expr.name), expr.levs)]
edit_expr(refs_list$meas)
edit_expr(refs_list$plot.ref)
plot(refs_list)+
theme(
axis.text.x=element_text(angle=30,hjust=1),
panel.spacing=grid::unit(1,"lines"))
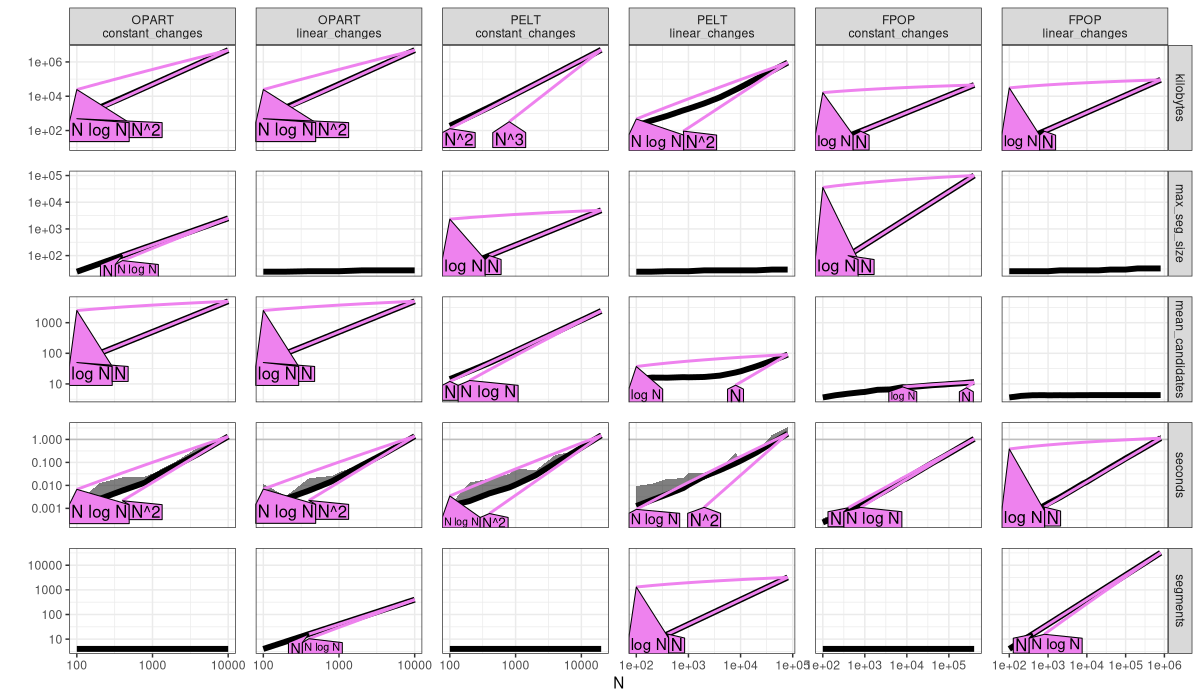
The plot above is an empirical verification of our earlier complexity claims.
- OPART
mean_candidatesis linear,O(N), and time and memory are quadratic,O(N^2). - PELT with constant changes has linear
mean_candidates,O(N), and quadratic time and memory,O(N^2)(same as OPART, no asymptotic speedup). - PELT with linear changes has sub-linear
mean_candidates(constant or log), and linear or log-linear time/memory. - FPOP always has sub-linear
mean_candidates(constant or log), and linear or log-linear time/memory.
The code/plot below shows the speedups in this case.
pred_list <- predict(refs_list)
ggplot()+
theme_bw()+
theme(
text=element_text(size=20))+
geom_line(aes(
N, empirical, color=expr.grid),
data=pred_list$measurements[unit=="seconds"])+
directlabels::geom_dl(aes(
N, unit.value, color=expr.grid, label=sprintf(
"%s\n%s\nN=%s",
expr.grid,
ifelse(expr.grid %in% c("FPOP","DUST"), "C++", "R"),
format(round(N), big.mark=",", scientific=FALSE, trim=TRUE))),
data=pred_list$prediction,
method=list(cex=1.5,"top.polygons"))+
scale_color_manual(
"algorithm",
guide="none",
values=algo.colors)+
facet_grid(. ~ simulation, scales="free", labeller=label_both)+
scale_x_log10(
"N = number of data in sequence",
breaks=10^seq(2,7),
limits=c(NA, 1e8))+
scale_y_log10(
"Computation time (seconds)",
breaks=10^seq(-3,0),
limits=10^c(-4,1))
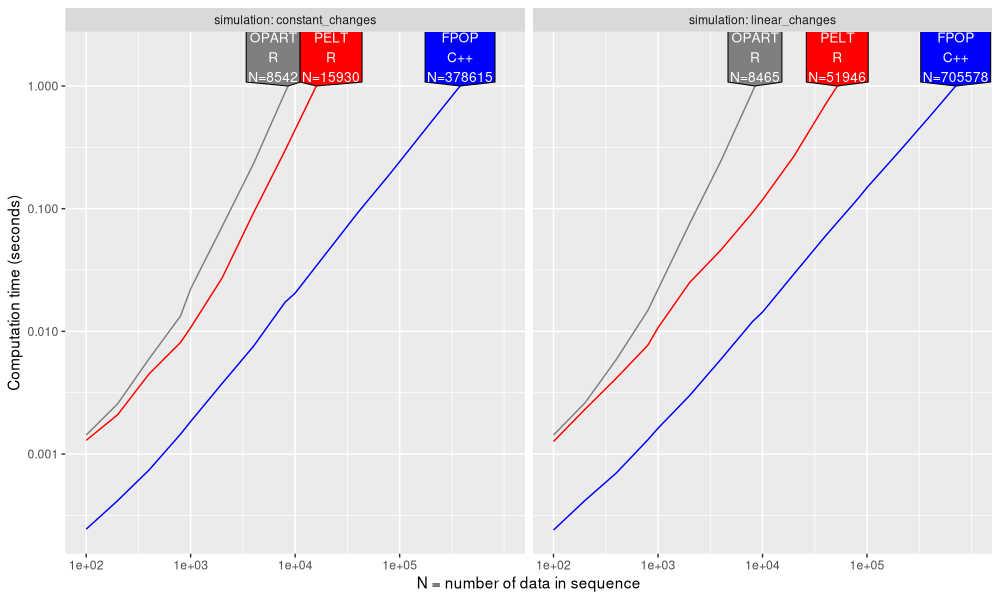
The figure above shows the throughput (data size N) which is possible to compute in 1 second using each algorithm. We see that FPOP is 10-100x faster than OPART/PELT. Part of the difference is that OPART/PELT were coded in R, whereas FPOP was coded in C++ (faster). Another difference is that FPOP is asymptotically faster with constant changes, as can be seen by a smaller slope for FPOP, compared to OPART/PELT.
Below we zoom in on the number of candidate change-points considered by each algorithm.
cand_dt <- pred_list$measurements[unit=="mean_candidates"]
ggplot()+
theme_bw()+
theme(
axis.text.x=element_text(size=20,angle=30,hjust=1),
text=element_text(size=20))+
geom_line(aes(
N, empirical, color=expr.grid),
data=cand_dt)+
directlabels::geom_dl(aes(
N, empirical, color=expr.grid, label=expr.grid),
data=cand_dt,
method=list(cex=2, "right.polygons"))+
scale_color_manual(
"algorithm",
guide="none",
values=algo.colors)+
facet_grid(. ~ simulation, scales="free", labeller=label_both)+
scale_x_log10(
"N = number of data in sequence",
breaks=10^seq(2,7,by=1),
limits=c(NA, 5e8))+
scale_y_log10("Mean number of candidate change-points")
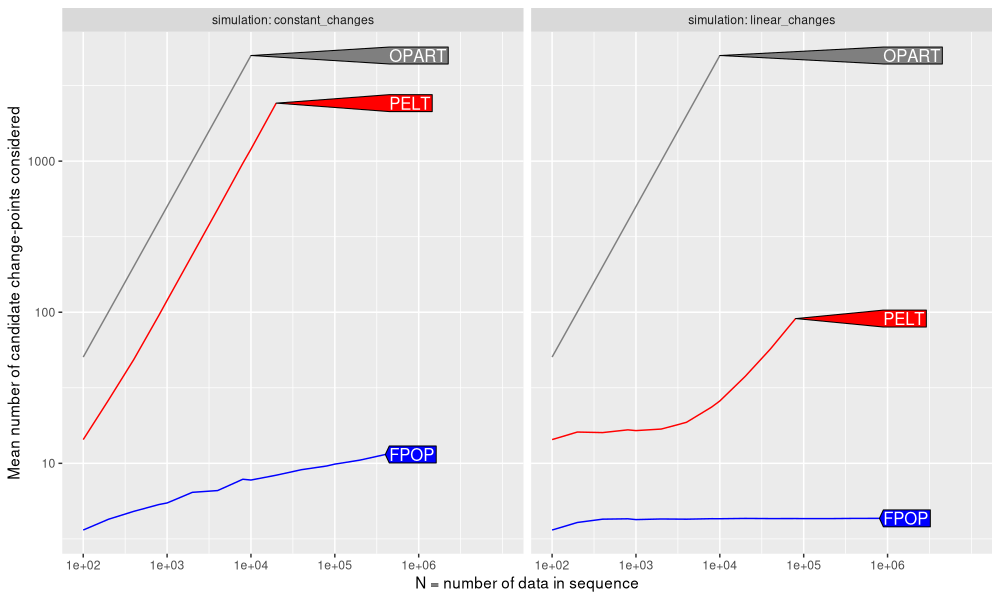
The figure above shows that
- OPART always considers a linear number of candidates (slow).
- PELT also considers a linear number of candidates (slow), when the number of changes is constant.
- PELT considers a sub-linear number of candidates (fast), when the number of changes is linear.
- FPOP always considers sub-linear number of candidates (fast), which is either constant for a linear number of changes, or logarithmic for a constant number of changes.
Conclusions
We have explored three algorithms for optimal change-point detection.
- The classic OPART algorithm is always quadratic time in the number of data to segment.
- The Pruned Exact Linear Time (PELT) algorithm can indeed be linear time in the number of data to segment, but only when the number of change-points grows with the number of data points. When the number of change-points is constant, there are ever-increasing segments, and the PELT algorithm must compute a cost for each candidate on these large segments; in this situation, PELT suffers from the same quadratic time complexity as OPART.
- The FPOP algorithm is fast (linear or log-linear) in both of the scenarios we examined.
We performed the comparison for count data (Poisson loss), but we could do something similar for real data (square loss), by modifying one of these implementations of dynamic programming:
Session info
sessionInfo()
## R version 4.5.0 (2025-04-11)
## Platform: x86_64-pc-linux-gnu
## Running under: Ubuntu 24.04.2 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.12.0
## LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.12.0 LAPACK version 3.12.0
##
## locale:
## [1] LC_CTYPE=fr_FR.UTF-8 LC_NUMERIC=C LC_TIME=fr_FR.UTF-8 LC_COLLATE=fr_FR.UTF-8
## [5] LC_MONETARY=fr_FR.UTF-8 LC_MESSAGES=fr_FR.UTF-8 LC_PAPER=fr_FR.UTF-8 LC_NAME=C
## [9] LC_ADDRESS=C LC_TELEPHONE=C LC_MEASUREMENT=fr_FR.UTF-8 LC_IDENTIFICATION=C
##
## time zone: Europe/Paris
## tzcode source: system (glibc)
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] ggplot2_3.5.1 data.table_1.17.0
##
## loaded via a namespace (and not attached):
## [1] directlabels_2024.1.21 vctrs_0.6.5 cli_3.6.4 knitr_1.50
## [5] rlang_1.1.5 xfun_0.51 penaltyLearning_2024.9.3 bench_1.1.4
## [9] generics_0.1.3 glue_1.8.0 labeling_0.4.3 colorspace_2.1-1
## [13] scales_1.3.0 quadprog_1.5-8 grid_4.5.0 munsell_0.5.1
## [17] evaluate_1.0.3 tibble_3.2.1 profmem_0.6.0 lifecycle_1.0.4
## [21] compiler_4.5.0 codetools_0.2-20 dplyr_1.1.4 dust_0.3.0
## [25] Rcpp_1.0.14 pkgconfig_2.0.3 PeakSegOptimal_2025.3.31 atime_2025.4.1
## [29] lattice_0.22-6 farver_2.1.2 R6_2.6.1 tidyselect_1.2.1
## [33] pillar_1.10.1 magrittr_2.0.3 tools_4.5.0 withr_3.0.2
## [37] gtable_0.3.6 remotes_2.5.0