Visualizing prediction error
In machine learning papers, we often need to compare the prediction error/accuracy of different algorithms. This post explains how to do that using data visualizations that are easy to read/interpret.
Example: gradient descent learning of binary classification models
Classification is a machine learning problem that has been widely studied for the last few decades. Binary classification is the special case when there are two possible classes to predict (spam vs normal email, cat vs dog in images, etc). To evaluate the prediction accuracy of learned binary classification models, we often use the Area Under the ROC Curve, because it allows fair comparison, even when the distribution of labels is unbalanced (for example, 1% positive/spam and 99% negative/normal email).
In our recent JMLR’23 paper, we proposed the AUM loss function, which can be used in gradient descent learning algorithms, to optimize ROC curves. Recently I did a computational experiment to compare this loss function to others, via the following setup.
- We were motivated by the following question: Can gradient descent using the AUM loss result in faster computation of a model with good generalization properties? (large AUC on held-out data)
- We wanted to compare the AUM loss to the standard Logistic/Cross-Entropy loss used in classification, as well as the all pairs squared hinge loss which is a popular relaxation of the Mann-Whitney U statistic (and therefore a surrogate for ROC-AUC, for more info see my paper with Kyle Rust).
- We analyzed four different image classification data sets, in which each had 10 classes. So in each data set we converted to a binary problem, by using the first class (0) as the negative/0 class, and using all of the other classes as the positive/1 class. So each data set had about 10% negative and 90% positive labels.
- Data sets had different numbers of features, so were down-sampled to different sizes, in order to get train times which were similar between data sets. For example STL10 had the largest number of features (27648), so had the smallest train set; MNIST with only 784 features had the largest train set.
- Source code used to compute the result, for a given loss function and learning rate, is in data_Classif.py
- We tried a range of learning rates,
10^seq(-4,5), and three different loss functions, as can be seen in data_Classif_batchtools.R. - For each algorithm, data set, random seed, and learning rate, we used torch to initialize a random linear model, and then did 100000 epochs of gradient descent learning with constant step size (learning rate).
- Then for each algorithm, data set, and random seed, we select only the epoch/iteration and step size that achieved the max AUC on the validation set.
The results can be read from data_Classif_batchtools_best_valid.csv, as shown in the code below:
library(data.table)
(best.dt <- fread("../assets/data_Classif_batchtools_best_valid.csv"))
## data.name N loss seed lr step_number loss_value auc
## <char> <int> <char> <int> <num> <int> <num> <num>
## 1: CIFAR10 5623 AUM 1 1e+00 45 5.196870e+01 0.8220866
## 2: CIFAR10 5623 AUM 2 1e+04 40 5.412949e+05 0.8192649
## 3: CIFAR10 5623 AUM 3 1e+05 55 4.929346e+06 0.8197657
## 4: CIFAR10 5623 AUM 4 1e+03 29 4.944706e+04 0.8211118
## 5: CIFAR10 5623 Logistic 1 1e+01 63 1.137827e+02 0.8084200
## 6: CIFAR10 5623 Logistic 2 1e+05 7 6.490934e+05 0.8177584
## 7: CIFAR10 5623 Logistic 3 1e+01 12 1.027919e+02 0.8096859
## 8: CIFAR10 5623 Logistic 4 1e+04 13 1.202190e+05 0.8072651
## 9: CIFAR10 5623 SquaredHinge 1 1e+03 1 1.744445e+07 0.7710211
## 10: CIFAR10 5623 SquaredHinge 2 1e+00 1 1.163525e+03 0.7354803
## 11: CIFAR10 5623 SquaredHinge 3 1e+00 8 2.199932e+09 0.7309735
## 12: CIFAR10 5623 SquaredHinge 4 1e+05 1 1.974501e+11 0.7753759
## 13: FashionMNIST 10000 AUM 1 1e+02 61 1.475747e+02 0.9817591
## 14: FashionMNIST 10000 AUM 2 1e+01 70 1.553757e+01 0.9816031
## 15: FashionMNIST 10000 AUM 3 1e+05 75 1.575107e+05 0.9818049
## 16: FashionMNIST 10000 AUM 4 1e+02 67 1.507560e+02 0.9820311
## 17: FashionMNIST 10000 Logistic 1 1e+00 397 8.089332e+00 0.9408162
## 18: FashionMNIST 10000 Logistic 2 1e+02 1125 6.918590e+02 0.9405631
## 19: FashionMNIST 10000 Logistic 3 1e+02 1213 6.432875e+02 0.9414778
## 20: FashionMNIST 10000 Logistic 4 1e+03 931 7.283925e+03 0.9408533
## 21: FashionMNIST 10000 SquaredHinge 1 1e+01 71 4.527093e-02 0.9781764
## 22: FashionMNIST 10000 SquaredHinge 2 1e+01 94 1.379243e-01 0.9808044
## 23: FashionMNIST 10000 SquaredHinge 3 1e+01 47 5.958961e-02 0.9759747
## 24: FashionMNIST 10000 SquaredHinge 4 1e+01 23 4.981834e-02 0.9650889
## 25: MNIST 18032 AUM 1 1e+01 28 3.038475e+00 0.9967078
## 26: MNIST 18032 AUM 2 1e+03 36 3.333767e+02 0.9967440
## 27: MNIST 18032 AUM 3 1e+03 29 2.631508e+02 0.9969475
## 28: MNIST 18032 AUM 4 1e+02 34 2.607299e+01 0.9970675
## 29: MNIST 18032 Logistic 1 1e+00 45322 7.714394e+00 0.9899026
## 30: MNIST 18032 Logistic 2 1e+00 44783 7.678055e+00 0.9898945
## 31: MNIST 18032 Logistic 3 1e+00 44620 7.705319e+00 0.9899023
## 32: MNIST 18032 Logistic 4 1e+00 44829 7.701845e+00 0.9901057
## 33: MNIST 18032 SquaredHinge 1 1e+02 215 1.577004e-02 0.9964240
## 34: MNIST 18032 SquaredHinge 2 1e+02 178 1.847402e-02 0.9968762
## 35: MNIST 18032 SquaredHinge 3 1e+02 158 1.802334e-02 0.9968006
## 36: MNIST 18032 SquaredHinge 4 1e+02 225 1.207210e-02 0.9969883
## 37: STL10 1778 AUM 1 1e+01 22 2.455220e+03 0.8432584
## 38: STL10 1778 AUM 2 1e+00 21 2.232408e+02 0.8457865
## 39: STL10 1778 AUM 3 1e+05 23 2.420980e+07 0.8483989
## 40: STL10 1778 AUM 4 1e+00 13 2.384768e+02 0.8461657
## 41: STL10 1778 Logistic 1 1e+03 17 1.080996e+05 0.8076966
## 42: STL10 1778 Logistic 2 1e+02 2 6.999322e+03 0.8243258
## 43: STL10 1778 Logistic 3 1e+03 5 1.096540e+05 0.8046910
## 44: STL10 1778 Logistic 4 1e+01 14 1.213560e+03 0.8106742
## 45: STL10 1778 SquaredHinge 1 1e-01 1 5.429723e+03 0.7627528
## 46: STL10 1778 SquaredHinge 2 1e+05 1 2.601109e+16 0.7589888
## 47: STL10 1778 SquaredHinge 3 1e+01 6 4.489175e+34 0.7541152
## 48: STL10 1778 SquaredHinge 4 1e-01 1 2.382808e+02 0.8266292
## data.name N loss seed lr step_number loss_value auc
Easy dot plot visualization
A visualization method which is simple to code is shown below:
library(ggplot2)
ggplot()+
geom_point(aes(
auc, loss),
data=best.dt)+
facet_grid(. ~ data.name)
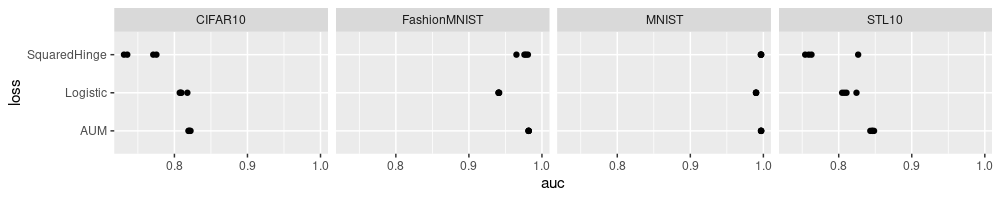
The plot above shows four dots for each loss and data set. Already we
can see that loss=AUM tends to have the largest auc values, in each
data set. Rather than showing the four data sets using the same X axis
scale, we can show more subtle differences, by allowing each data set
to have its own X axis scale, as below.
ggplot()+
geom_point(aes(
auc, loss),
data=best.dt)+
facet_grid(. ~ data.name, scales="free", labeller=label_both)
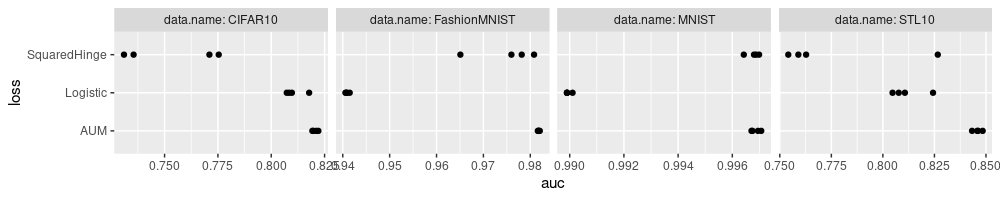
Above we see each data set has its own scale, but some of the tick marks are not readable. This can be fixed by specifying non-default panel spacing values in the theme, as below.
ggplot()+
geom_point(aes(
auc, loss),
data=best.dt)+
facet_grid(. ~ data.name, scales="free", labeller=label_both)+
theme(
panel.spacing=grid::unit(1.5, "lines"))
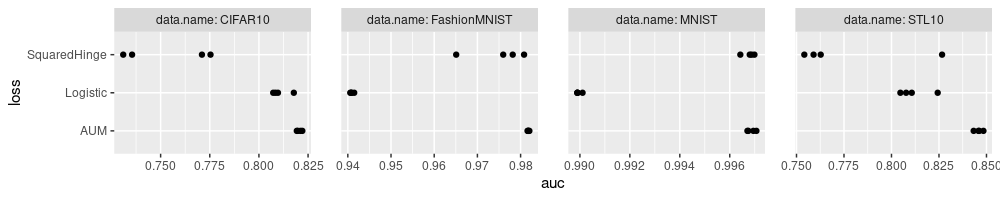
In the plot above there is now another issue: the last X tick mark goes off the right edge of the plot. To fix that we need to adjust the plot margin, as below.
ggplot()+
geom_point(aes(
auc, loss),
data=best.dt)+
facet_grid(. ~ data.name, scales="free", labeller=label_both)+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))
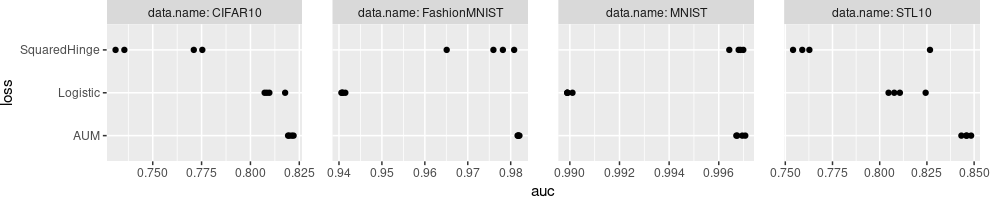
The plot above looks like a reasonable summary of the results, but the labels could be improved.
- We could explain more details about each algorithm in the Y axis labels.
- We could simplify the panel/facet variable names,
data.nameabove, to simplyData, and addNfor each. - We could use the more common capital
AUCrather than lowerauc, and explain that it is the max on the validation set.
loss2show <- rev(c(
Logistic="Logistic/Cross-entropy\n(classic baseline)",
SquaredHinge="All Pairs Squared Hinge\n(recent alternative)",
AUM="AUM=Area Under Min(FP,FN)\n(proposed complex loss)",
NULL))
Loss_factor <- function(L){
factor(L, names(loss2show), loss2show)
}
best.dt[, `:=`(
Loss = Loss_factor(loss),
Data = data.name
)]
ggplot()+
geom_point(aes(
auc, Loss),
data=best.dt)+
facet_grid(. ~ N + Data, scales="free", labeller=label_both)+
scale_x_continuous(
"Max validation AUC (4 random initializations)")+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))
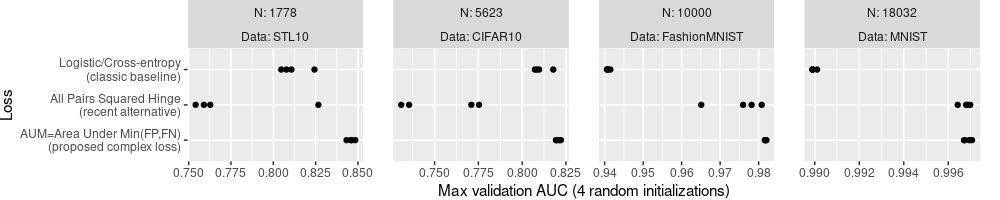
Note the Loss names in code above is arranged to be consistent with
their display in the plot above: the Loss column factor levels come
from loss2show, and are used to determine the order of display of
the tick marks in the Y axis.
Similarly, the facets/panels are ordered by the first facet variable,
N (smallest N for STL10 on the left, largest N for MNIST on the
right). This order is different than previous plots, which had facets
in alphabetical order (CIFAR10 left, STL10 right). To display an
alternative facet/panel order, you would have to create a factor
variable with the levels in the desired order, similar to what we did
with Loss values for the Y axis above. (exercise for the reader)
Display mean and standard deviation
Whereas in the previous section we displayed each random seed as a different dot, below we compute and plot the mean and SD over random seeds. And while we are at it, we can also compute the range (min and max), for the AUC as well as for the number of gradient descent epochs (which is the same as the number of steps here, since we used full gradient method, batch size = N).
(best.wide <- dcast(
best.dt,
N + Data + Loss ~ .,
list(mean, sd, length, min, max),
value.var=c("auc","step_number")))
## Key: <N, Data, Loss>
## N Data Loss auc_mean step_number_mean auc_sd
## <int> <char> <fctr> <num> <num> <num>
## 1: 1778 STL10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.8459024 19.75 0.0021060041
## 2: 1778 STL10 All Pairs Squared Hinge\n(recent alternative) 0.7756215 2.25 0.0341884983
## 3: 1778 STL10 Logistic/Cross-entropy\n(classic baseline) 0.8118469 9.50 0.0086704638
## 4: 5623 CIFAR10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.8205572 42.25 0.0012836241
## 5: 5623 CIFAR10 All Pairs Squared Hinge\n(recent alternative) 0.7532127 2.75 0.0232189982
## 6: 5623 CIFAR10 Logistic/Cross-entropy\n(classic baseline) 0.8107824 23.75 0.0047546328
## 7: 10000 FashionMNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.9817996 68.25 0.0001768922
## 8: 10000 FashionMNIST All Pairs Squared Hinge\n(recent alternative) 0.9750111 58.75 0.0069031630
## 9: 10000 FashionMNIST Logistic/Cross-entropy\n(classic baseline) 0.9409276 916.50 0.0003887880
## 10: 18032 MNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.9968667 31.75 0.0001704442
## 11: 18032 MNIST All Pairs Squared Hinge\n(recent alternative) 0.9967723 194.00 0.0002446508
## 12: 18032 MNIST Logistic/Cross-entropy\n(classic baseline) 0.9899513 44888.50 0.0001030444
## step_number_sd auc_length step_number_length auc_min step_number_min auc_max step_number_max
## <num> <int> <int> <num> <int> <num> <int>
## 1: 4.573474 4 4 0.8432584 13 0.8483989 23
## 2: 2.500000 4 4 0.7541152 1 0.8266292 6
## 3: 7.141428 4 4 0.8046910 2 0.8243258 17
## 4: 10.812801 4 4 0.8192649 29 0.8220866 55
## 5: 3.500000 4 4 0.7309735 1 0.7753759 8
## 6: 26.297972 4 4 0.8072651 7 0.8177584 63
## 7: 5.852350 4 4 0.9816031 61 0.9820311 75
## 8: 30.598203 4 4 0.9650889 23 0.9808044 94
## 9: 365.820994 4 4 0.9405631 397 0.9414778 1213
## 10: 3.862210 4 4 0.9967078 28 0.9970675 36
## 11: 31.379399 4 4 0.9964240 158 0.9969883 225
## 12: 302.591584 4 4 0.9898945 44620 0.9901057 45322
In the result table above, we also compute the length to double
check that the mean/etc was indeed taken over the four random seeds.
The code/plot below only uses the mean.
ggplot()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_x_continuous(
"Max validation AUC (Mean over 4 random initializations)")
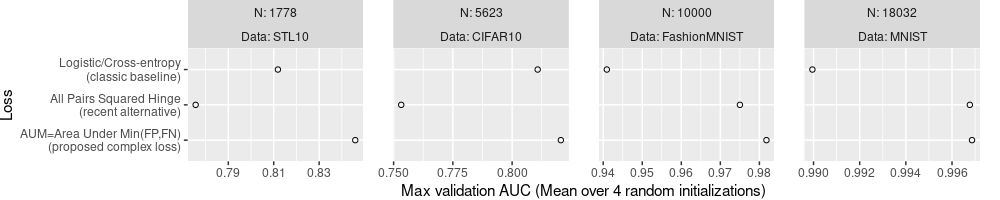
The plot above is not very useful for comparing the different Loss
functions, because it only shows the mean, without showing any measure
of the variance. So we can not say if any Loss is significantly more
or less accurate than any other (we would need error bars or
confidence intervals to do that). We fix that in the code/plot below,
by computing lo and hi limits to display based on the SD.
best.wide[, `:=`(
lo = auc_mean-auc_sd,
hi = auc_mean+auc_sd
)]
ggplot()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
lo, Loss,
xend=hi, yend=Loss),
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_x_continuous(
"Max validation AUC (Mean ± SD over 4 random initializations)")
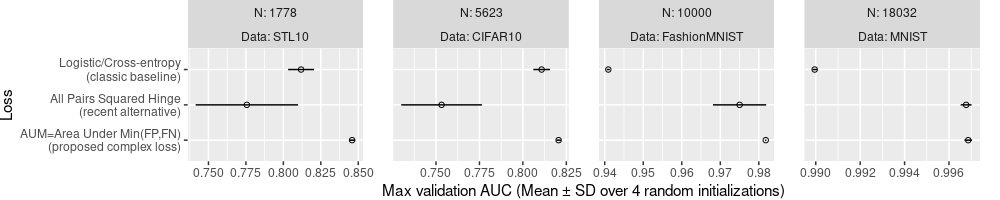
The plot above is much better, because it shows the SD as well as the mean. We can see that AUM is significantly more accurate than the others in all of the data sets, except perhaps MNIST, in which the All Pairs Squared Hinge looks only slightly worse. We could additionally write the values of mean and SD, as below.
ggplot()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
lo, Loss,
xend=hi, yend=Loss),
data=best.wide)+
geom_text(aes(
auc_mean, Loss,
label=sprintf(
"%.4f±%.4f", auc_mean, auc_sd)),
size=3,
vjust=1.5,
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_x_continuous(
"Max validation AUC (Mean ± SD over 4 random initializations)")
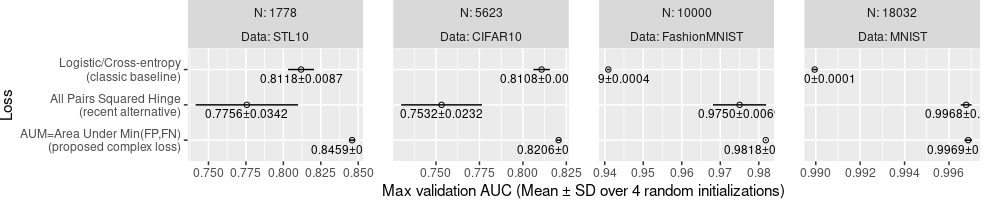
Above, only some of the text is readable, and others go outside of the panels.
To fix this, we can use aes(hjust):
- The default
hjust=0.5, used in the plot above, draws the text centered around the mean value. - if the mean is less than the mid point of the panel X axis, then we
can use
hjust=0which means text will be left justified with the mean value as the limit. In other words, the text will start writing from the mean value, and go to the right of the mean value, but is guaranteed to not go left of the mean value, so it will not go off the panel to the left. - otherwise, we can use
hjust=1which means text will be right justified to the mean value.
To get this scheme to work, we need to compute the mid-point on the X axis (auc) of each panel, which we do in the code below.
best.wide[
, mid := (min(lo)+max(hi))/2
, by=Data]
ggplot()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
lo, Loss,
xend=hi, yend=Loss),
data=best.wide)+
geom_text(aes(
auc_mean, Loss,
hjust=ifelse(auc_mean<mid, 0, 1),
label=sprintf(
"%.4f±%.4f", auc_mean, auc_sd)),
size=3,
vjust=1.5,
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_x_continuous(
"Max validation AUC (Mean ± SD over 4 random initializations)")
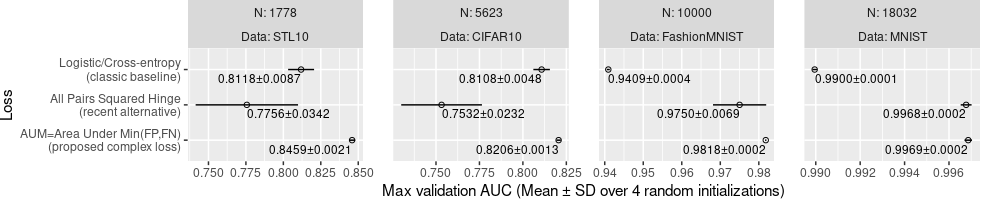
The plot above has text that can be read to determine the mean and SD values of each loss, in each data set.
P-value plot
To conclusively answer the question about whether AUM results in larger Max validation AUC than the next best loss, we would need to use a statistical significance test. First we compute the best two loss functions for each dataset, as below.
(best.two <- best.wide[
order(N,-auc_mean)
][
, rank := rank(-auc_mean)
, by=.(N,Data)
][rank <= 2, .(N,Data,Loss,auc_mean,rank)])
## N Data Loss auc_mean rank
## <int> <char> <fctr> <num> <num>
## 1: 1778 STL10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.8459024 1
## 2: 1778 STL10 Logistic/Cross-entropy\n(classic baseline) 0.8118469 2
## 3: 5623 CIFAR10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.8205572 1
## 4: 5623 CIFAR10 Logistic/Cross-entropy\n(classic baseline) 0.8107824 2
## 5: 10000 FashionMNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.9817996 1
## 6: 10000 FashionMNIST All Pairs Squared Hinge\n(recent alternative) 0.9750111 2
## 7: 18032 MNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 0.9968667 1
## 8: 18032 MNIST All Pairs Squared Hinge\n(recent alternative) 0.9967723 2
Below we join with the original data.
(best.two.join <- best.dt[best.two, .(N,Data,Loss,rank,seed,auc), on=.(N,Data,Loss)])
## N Data Loss rank seed auc
## <int> <char> <fctr> <num> <int> <num>
## 1: 1778 STL10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 1 0.8432584
## 2: 1778 STL10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 2 0.8457865
## 3: 1778 STL10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 3 0.8483989
## 4: 1778 STL10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 4 0.8461657
## 5: 1778 STL10 Logistic/Cross-entropy\n(classic baseline) 2 1 0.8076966
## 6: 1778 STL10 Logistic/Cross-entropy\n(classic baseline) 2 2 0.8243258
## 7: 1778 STL10 Logistic/Cross-entropy\n(classic baseline) 2 3 0.8046910
## 8: 1778 STL10 Logistic/Cross-entropy\n(classic baseline) 2 4 0.8106742
## 9: 5623 CIFAR10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 1 0.8220866
## 10: 5623 CIFAR10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 2 0.8192649
## 11: 5623 CIFAR10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 3 0.8197657
## 12: 5623 CIFAR10 AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 4 0.8211118
## 13: 5623 CIFAR10 Logistic/Cross-entropy\n(classic baseline) 2 1 0.8084200
## 14: 5623 CIFAR10 Logistic/Cross-entropy\n(classic baseline) 2 2 0.8177584
## 15: 5623 CIFAR10 Logistic/Cross-entropy\n(classic baseline) 2 3 0.8096859
## 16: 5623 CIFAR10 Logistic/Cross-entropy\n(classic baseline) 2 4 0.8072651
## 17: 10000 FashionMNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 1 0.9817591
## 18: 10000 FashionMNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 2 0.9816031
## 19: 10000 FashionMNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 3 0.9818049
## 20: 10000 FashionMNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 4 0.9820311
## 21: 10000 FashionMNIST All Pairs Squared Hinge\n(recent alternative) 2 1 0.9781764
## 22: 10000 FashionMNIST All Pairs Squared Hinge\n(recent alternative) 2 2 0.9808044
## 23: 10000 FashionMNIST All Pairs Squared Hinge\n(recent alternative) 2 3 0.9759747
## 24: 10000 FashionMNIST All Pairs Squared Hinge\n(recent alternative) 2 4 0.9650889
## 25: 18032 MNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 1 0.9967078
## 26: 18032 MNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 2 0.9967440
## 27: 18032 MNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 3 0.9969475
## 28: 18032 MNIST AUM=Area Under Min(FP,FN)\n(proposed complex loss) 1 4 0.9970675
## 29: 18032 MNIST All Pairs Squared Hinge\n(recent alternative) 2 1 0.9964240
## 30: 18032 MNIST All Pairs Squared Hinge\n(recent alternative) 2 2 0.9968762
## 31: 18032 MNIST All Pairs Squared Hinge\n(recent alternative) 2 3 0.9968006
## 32: 18032 MNIST All Pairs Squared Hinge\n(recent alternative) 2 4 0.9969883
## N Data Loss rank seed auc
Below we reshape, which is required before doing the T-test in R.
(best.two.wide <- dcast(best.two.join, N+Data+seed~rank, value.var="auc"))
## Key: <N, Data, seed>
## N Data seed 1 2
## <int> <char> <int> <num> <num>
## 1: 1778 STL10 1 0.8432584 0.8076966
## 2: 1778 STL10 2 0.8457865 0.8243258
## 3: 1778 STL10 3 0.8483989 0.8046910
## 4: 1778 STL10 4 0.8461657 0.8106742
## 5: 5623 CIFAR10 1 0.8220866 0.8084200
## 6: 5623 CIFAR10 2 0.8192649 0.8177584
## 7: 5623 CIFAR10 3 0.8197657 0.8096859
## 8: 5623 CIFAR10 4 0.8211118 0.8072651
## 9: 10000 FashionMNIST 1 0.9817591 0.9781764
## 10: 10000 FashionMNIST 2 0.9816031 0.9808044
## 11: 10000 FashionMNIST 3 0.9818049 0.9759747
## 12: 10000 FashionMNIST 4 0.9820311 0.9650889
## 13: 18032 MNIST 1 0.9967078 0.9964240
## 14: 18032 MNIST 2 0.9967440 0.9968762
## 15: 18032 MNIST 3 0.9969475 0.9968006
## 16: 18032 MNIST 4 0.9970675 0.9969883
Below we run T-tests to see if the top ranked AUC is significantly greater than the next ranked AUC, for each data set.
(test.dt <- best.two.wide[, {
paired <- t.test(`1`, `2`, alternative="greater", paired=TRUE)
unpaired <- t.test(`1`, `2`, alternative="greater", paired=FALSE)
data.table(
mean.of.diff=paired$estimate, p.paired=paired$p.value,
m1=unpaired$estimate[1], m2=unpaired$estimate[2], p.unpaired=unpaired$p.value)
}, by=.(N,Data)])
## Key: <N, Data>
## N Data mean.of.diff p.paired m1 m2 p.unpaired
## <int> <char> <num> <num> <num> <num> <num>
## 1: 1778 STL10 3.405548e-02 0.00258075 0.8459024 0.8118469 0.001564229
## 2: 5623 CIFAR10 9.774872e-03 0.02149806 0.8205572 0.8107824 0.011088867
## 3: 10000 FashionMNIST 6.788444e-03 0.07539559 0.9817996 0.9750111 0.071935081
## 4: 18032 MNIST 9.439573e-05 0.17791682 0.9968667 0.9967723 0.276335600
The table above summarizes the results of the T-tests.
- The paired T-test is more powerful (gives you smaller P-values), but
only works when you actually have paired observations, as we do here
(AUC was computed for each loss and each random seed). Its
estimateis the mean of the differences between each pair of AUC values. - The unpaired T-test can be seen to have larger (less significant)
P-values, but it may be useful to run as well, because
estimatecontains mean values for each of the two samples (here the two different loss functions).
To display the test result below we use a rectangle.
p.color <- "red"
text.size <- 3
ggplot()+
theme_bw()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_rect(aes(
xmin=m2, xmax=m1,
ymin=-Inf, ymax=Inf),
fill=p.color,
alpha=0.5,
data=test.dt)+
geom_text(aes(
m1, Inf, label=sprintf("Diff=%.4f P=%.4f ", mean.of.diff, p.paired)),
data=test.dt,
size=text.size,
vjust=1.2,
hjust=1)+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
lo, Loss,
xend=hi, yend=Loss),
data=best.wide)+
geom_text(aes(
auc_mean, Loss,
hjust=ifelse(auc_mean<mid, 0, 1),
label=sprintf(
"%.4f±%.4f", auc_mean, auc_sd)),
size=text.size,
vjust=1.5,
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_y_discrete(
"Loss")+
scale_x_continuous(
"Max validation AUC (Mean ± SD over 4 random initializations)")
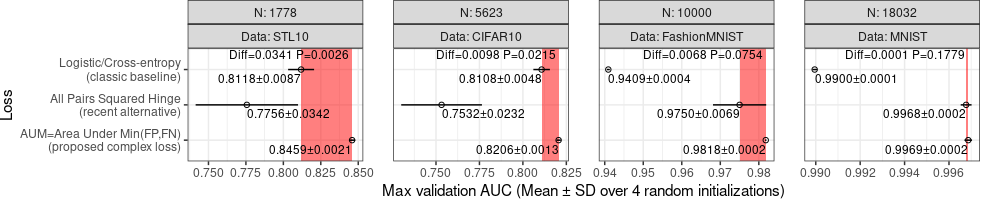
In the plot above, we show the p-value, which is typically intepreted by comparing with the traditional significance threshold of 0.05, which corresponds to a 5% false positive rate. Seeing a p-value of 0.05 means that you have observed a difference that you would see about 5% of the time (simply due to random variation/noise), if there is really no difference between methods. So if we are trying to argue that one algorithm is better, then we want to see small p-values, which mean that we have observed differences that are so large, that it would be extremely unlikely to see such a difference by random chance.
- in STL10 there is a highly significant difference (p=0.002, order of magnitude less than 0.05).
- in CIFAR10 there is a significant difference (p=0.02 is less than 0.05),
- in FashionMNIST there is a slight difference (but we do not say significant because p=0.07 is still larger than 0.05),
- the difference in MNIST is not statistically significant (p=0.17 much larger than 0.05),
Above we compared the best to the next best. An alternative is to compare the proposed to others, which we code below. First we reshape wider, as below.
(best.loss.wide <- dcast(best.dt, N + Data + seed ~ loss, value.var="auc"))
## Key: <N, Data, seed>
## N Data seed AUM Logistic SquaredHinge
## <int> <char> <int> <num> <num> <num>
## 1: 1778 STL10 1 0.8432584 0.8076966 0.7627528
## 2: 1778 STL10 2 0.8457865 0.8243258 0.7589888
## 3: 1778 STL10 3 0.8483989 0.8046910 0.7541152
## 4: 1778 STL10 4 0.8461657 0.8106742 0.8266292
## 5: 5623 CIFAR10 1 0.8220866 0.8084200 0.7710211
## 6: 5623 CIFAR10 2 0.8192649 0.8177584 0.7354803
## 7: 5623 CIFAR10 3 0.8197657 0.8096859 0.7309735
## 8: 5623 CIFAR10 4 0.8211118 0.8072651 0.7753759
## 9: 10000 FashionMNIST 1 0.9817591 0.9408162 0.9781764
## 10: 10000 FashionMNIST 2 0.9816031 0.9405631 0.9808044
## 11: 10000 FashionMNIST 3 0.9818049 0.9414778 0.9759747
## 12: 10000 FashionMNIST 4 0.9820311 0.9408533 0.9650889
## 13: 18032 MNIST 1 0.9967078 0.9899026 0.9964240
## 14: 18032 MNIST 2 0.9967440 0.9898945 0.9968762
## 15: 18032 MNIST 3 0.9969475 0.9899023 0.9968006
## 16: 18032 MNIST 4 0.9970675 0.9901057 0.9969883
The table above has one column for each method/loss. Then we define the proposed method column, and reshape the other columns taller, as below.
proposed.loss <- "AUM"
(other.loss.vec <- best.dt[loss!=proposed.loss, unique(loss)])
## [1] "Logistic" "SquaredHinge"
(best.loss.tall <- melt(
best.loss.wide,
measure.vars=other.loss.vec,
variable.name="other.loss",
value.name="other.auc"))
## N Data seed AUM other.loss other.auc
## <int> <char> <int> <num> <fctr> <num>
## 1: 1778 STL10 1 0.8432584 Logistic 0.8076966
## 2: 1778 STL10 2 0.8457865 Logistic 0.8243258
## 3: 1778 STL10 3 0.8483989 Logistic 0.8046910
## 4: 1778 STL10 4 0.8461657 Logistic 0.8106742
## 5: 5623 CIFAR10 1 0.8220866 Logistic 0.8084200
## 6: 5623 CIFAR10 2 0.8192649 Logistic 0.8177584
## 7: 5623 CIFAR10 3 0.8197657 Logistic 0.8096859
## 8: 5623 CIFAR10 4 0.8211118 Logistic 0.8072651
## 9: 10000 FashionMNIST 1 0.9817591 Logistic 0.9408162
## 10: 10000 FashionMNIST 2 0.9816031 Logistic 0.9405631
## 11: 10000 FashionMNIST 3 0.9818049 Logistic 0.9414778
## 12: 10000 FashionMNIST 4 0.9820311 Logistic 0.9408533
## 13: 18032 MNIST 1 0.9967078 Logistic 0.9899026
## 14: 18032 MNIST 2 0.9967440 Logistic 0.9898945
## 15: 18032 MNIST 3 0.9969475 Logistic 0.9899023
## 16: 18032 MNIST 4 0.9970675 Logistic 0.9901057
## 17: 1778 STL10 1 0.8432584 SquaredHinge 0.7627528
## 18: 1778 STL10 2 0.8457865 SquaredHinge 0.7589888
## 19: 1778 STL10 3 0.8483989 SquaredHinge 0.7541152
## 20: 1778 STL10 4 0.8461657 SquaredHinge 0.8266292
## 21: 5623 CIFAR10 1 0.8220866 SquaredHinge 0.7710211
## 22: 5623 CIFAR10 2 0.8192649 SquaredHinge 0.7354803
## 23: 5623 CIFAR10 3 0.8197657 SquaredHinge 0.7309735
## 24: 5623 CIFAR10 4 0.8211118 SquaredHinge 0.7753759
## 25: 10000 FashionMNIST 1 0.9817591 SquaredHinge 0.9781764
## 26: 10000 FashionMNIST 2 0.9816031 SquaredHinge 0.9808044
## 27: 10000 FashionMNIST 3 0.9818049 SquaredHinge 0.9759747
## 28: 10000 FashionMNIST 4 0.9820311 SquaredHinge 0.9650889
## 29: 18032 MNIST 1 0.9967078 SquaredHinge 0.9964240
## 30: 18032 MNIST 2 0.9967440 SquaredHinge 0.9968762
## 31: 18032 MNIST 3 0.9969475 SquaredHinge 0.9968006
## 32: 18032 MNIST 4 0.9970675 SquaredHinge 0.9969883
## N Data seed AUM other.loss other.auc
The table above has a column for the Max Validation AUC of the proposed method (AUM), and has the Max Validation AUC of the other methods in the other.auc column. We can then run the T-test for each value of other.loss, using the code below.
(test.proposed <- best.loss.tall[, {
paired <- t.test(AUM, other.auc, alternative="greater", paired=TRUE)
unpaired <- t.test(AUM, other.auc, alternative="greater", paired=FALSE)
data.table(
mean.of.diff=paired$estimate, p.paired=paired$p.value,
mean.proposed=unpaired$estimate[1], mean.other=unpaired$estimate[2], p.unpaired=unpaired$p.value)
}, by=.(N,Data,other.loss)])
## N Data other.loss mean.of.diff p.paired mean.proposed mean.other p.unpaired
## <int> <char> <fctr> <num> <num> <num> <num> <num>
## 1: 1778 STL10 Logistic 3.405548e-02 2.580750e-03 0.8459024 0.8118469 1.564229e-03
## 2: 5623 CIFAR10 Logistic 9.774872e-03 2.149806e-02 0.8205572 0.8107824 1.108887e-02
## 3: 10000 FashionMNIST Logistic 4.087194e-02 1.071213e-07 0.9817996 0.9409276 1.010710e-09
## 4: 18032 MNIST Logistic 6.915422e-03 5.360106e-07 0.9968667 0.9899513 7.150765e-09
## 5: 1778 STL10 SquaredHinge 7.028090e-02 1.313712e-02 0.8459024 0.7756215 1.290625e-02
## 6: 5623 CIFAR10 SquaredHinge 6.734453e-02 4.423756e-03 0.8205572 0.7532127 5.033883e-03
## 7: 10000 FashionMNIST SquaredHinge 6.788444e-03 7.539559e-02 0.9817996 0.9750111 7.193508e-02
## 8: 18032 MNIST SquaredHinge 9.439573e-05 1.779168e-01 0.9968667 0.9967723 2.763356e-01
The table above has a row for each T-test, one for each data set and other loss function (other than the proposed AUM). The final step is to visualize these data on the plot, as in the code below.
test.proposed[
, other.Loss := Loss_factor(other.loss)
]
ggplot()+
theme_bw()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_segment(aes(
mean.proposed, other.Loss,
xend=mean.other, yend=other.Loss),
color=p.color,
alpha=0.5,
linewidth=3,
data=test.proposed)+
geom_text(aes(
mean.proposed, other.Loss,
label=sprintf("Diff=%.4f P=%.4f", mean.of.diff, p.paired)),
color=p.color,
size=text.size,
vjust=-0.5,
hjust=1,
data=test.proposed)+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
lo, Loss,
xend=hi, yend=Loss),
data=best.wide)+
geom_text(aes(
auc_mean, Loss,
hjust=ifelse(auc_mean<mid, 0, 1),
label=sprintf(
"%.4f±%.4f", auc_mean, auc_sd)),
size=text.size,
vjust=1.5,
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_y_discrete(
"Loss")+
scale_x_continuous(
"Max validation AUC (Mean ± SD over 4 random initializations)")

We can see in the plot above that there is red text and segments drawn to emphasize the p-value, and how it was computed, for each method other than the proposed AUM. There are a couple of issues though
- The Y axis tick mark ordering is no longer as expected, because ggplot2 drops factor levels by default, if some are not present in a given data layer. To avoid that we can use
scale_y_discrete(drop=FALSE). - Some p-values are smaller than the limit of 4 decimal places, so we need a different method to display them, for example writing
P<0.0001when that is true.
ggplot()+
theme_bw()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
panel.spacing=grid::unit(1.5, "lines"))+
geom_segment(aes(
mean.proposed, other.Loss,
xend=mean.other, yend=other.Loss),
color=p.color,
alpha=0.5,
linewidth=3,
data=test.proposed)+
geom_text(aes(
mean.proposed, other.Loss,
label=paste(
sprintf("Diff=%.4f", mean.of.diff),
ifelse(
p.paired<0.0001, "P<0.0001",
sprintf("P=%.4f", p.paired)))),
color=p.color,
size=text.size,
vjust=-0.5,
hjust=1,
data=test.proposed)+
geom_point(aes(
auc_mean, Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
lo, Loss,
xend=hi, yend=Loss),
data=best.wide)+
geom_text(aes(
auc_mean, Loss,
hjust=ifelse(auc_mean<mid, 0, 1),
label=sprintf(
"%.4f±%.4f", auc_mean, auc_sd)),
size=text.size,
vjust=1.5,
data=best.wide)+
facet_grid(. ~ N + Data, labeller=label_both, scales="free")+
scale_y_discrete(
"Loss",
drop=FALSE)+
scale_x_continuous(
"Max validation AUC (Mean ± SD over 4 random initializations)")

Also note the code below, which provides an alternative method for computing the p-values:
best.dt[, {
proposed <- auc[loss=="AUM"]
.SD[
i = loss!="AUM",
j = t.test(proposed, auc, alternative="g")["p.value"],
by = loss]
}, by = .(N,Data)][order(loss,N)]
## N Data loss p.value
## <int> <char> <char> <num>
## 1: 1778 STL10 Logistic 1.564229e-03
## 2: 5623 CIFAR10 Logistic 1.108887e-02
## 3: 10000 FashionMNIST Logistic 1.010710e-09
## 4: 18032 MNIST Logistic 7.150765e-09
## 5: 1778 STL10 SquaredHinge 1.290625e-02
## 6: 5623 CIFAR10 SquaredHinge 5.033883e-03
## 7: 10000 FashionMNIST SquaredHinge 7.193508e-02
## 8: 18032 MNIST SquaredHinge 2.763356e-01
Display accuracy and computation time in scatter plot
In the plots above, we only examined prediction accuracy. Below we additionally examine the number of iterations/epochs of gradient descent, in order to determine which loss function results in fastest learning.
ggplot()+
theme_bw()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
legend.key.spacing.y=grid::unit(1, "lines"),
axis.text.x=element_text(angle=30, hjust=1),
panel.spacing=grid::unit(1.5, "lines"))+
geom_point(aes(
auc_mean, step_number_mean,
color=Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
auc_min, step_number_mean,
color=Loss,
xend=auc_max, yend=step_number_mean),
data=best.wide)+
geom_segment(aes(
auc_mean, step_number_min,
color=Loss,
xend=auc_mean, yend=step_number_max),
data=best.wide)+
facet_grid(~N+Data, labeller=label_both, scales="free")+
scale_y_log10(
"Gradient descent epochs\n(using best learning rate)")+
scale_x_continuous(
"Best validation AUC (dot=mean, segments=range over 4 random initializations)")
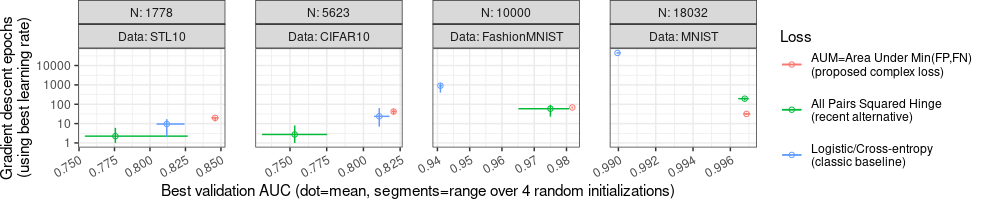
In the plot above, we again see Best validation AUC on the X axis, and we see number of epochs on the Y axis. So we can see that the AUM loss has largest Best validation AUC (so AUM can be more accurate), as well as comparable/smaller number of epochs (so AUM can be faster).
The plot above uses facet_grid which forces the Y axis to be the
same in each plot, even though we specified scales="free" (which
actually only affects the X axis in this case). Below we use
facet_wrap instead, in order to zoom in on the details of each
panel:
ggplot()+
theme_bw()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
legend.key.spacing.y=grid::unit(1, "lines"),
axis.text.x=element_text(angle=30, hjust=1),
panel.spacing=grid::unit(1.5, "lines"))+
geom_point(aes(
auc_mean, step_number_mean,
color=Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
auc_min, step_number_mean,
color=Loss,
xend=auc_max, yend=step_number_mean),
data=best.wide)+
geom_segment(aes(
auc_mean, step_number_min,
color=Loss,
xend=auc_mean, yend=step_number_max),
data=best.wide)+
facet_wrap(~N+Data, nrow=1, labeller=label_both, scales="free")+
scale_y_log10(
"Gradient descent epochs\n(using best learning rate)")+
scale_x_continuous(
"Best validation AUC (dot=mean, segments=range over 4 random initializations)")
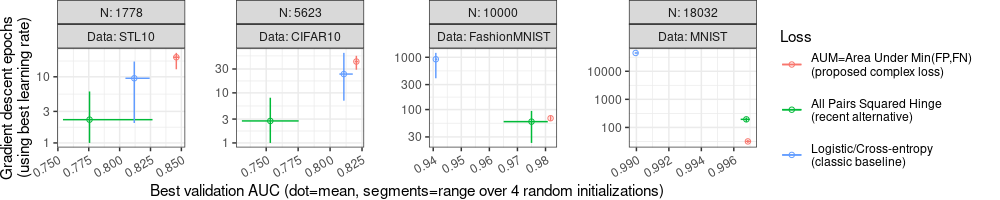
The plot above has a different Y axis for each panel/facet, due to facet_wrap(scales="free").
This allows us to zoom in to see more detailed comparisons in each panel/facet.
However there are a couple of details worth fixing, for improved clarity:
- The default color scale in ggplot2 results in a blue and green which can be difficult to distinguish, so I recommend using Cynthia Brewer’s color palettes, such as Dark2.
- Some data/segments go outside the range of the Y axis ticks, which
can make the Y axis difficult to read, so we can use
geom_blankto increase the Y axis range.
dput(RColorBrewer::brewer.pal(3,"Dark2"))
## c("#1B9E77", "#D95F02", "#7570B3")
loss.colors <- c("black", "#D95F02", "#7570B3")
names(loss.colors) <- loss2show
p <- function(Data,x,y)data.table(Data,x,y)
(blank.Data <- rbind(
p("CIFAR10",0.8,100),
p("MNIST",0.99,c(10,100000)),
p("STL10",0.8,30)))
## Data x y
## <char> <num> <num>
## 1: CIFAR10 0.80 1e+02
## 2: MNIST 0.99 1e+01
## 3: MNIST 0.99 1e+05
## 4: STL10 0.80 3e+01
(blank.Data.N <- best.wide[, .(N,Data)][blank.Data, on=.(Data), mult="first"])
## N Data x y
## <int> <char> <num> <num>
## 1: 5623 CIFAR10 0.80 1e+02
## 2: 18032 MNIST 0.99 1e+01
## 3: 18032 MNIST 0.99 1e+05
## 4: 1778 STL10 0.80 3e+01
ggplot()+
theme_bw()+
theme(
plot.margin=grid::unit(c(0,1,0,0), "lines"),
legend.key.spacing.y=grid::unit(1, "lines"),
axis.text.x=element_text(angle=30, hjust=1),
panel.spacing=grid::unit(1.5, "lines"))+
geom_blank(aes(x, y), data=blank.Data.N)+
geom_point(aes(
auc_mean, step_number_mean,
color=Loss),
shape=1,
data=best.wide)+
geom_segment(aes(
auc_min, step_number_mean,
color=Loss,
xend=auc_max, yend=step_number_mean),
data=best.wide)+
geom_segment(aes(
auc_mean, step_number_min,
color=Loss,
xend=auc_mean, yend=step_number_max),
data=best.wide)+
facet_wrap(~N+Data, nrow=1, labeller=label_both, scales="free")+
scale_color_manual(
values=loss.colors)+
scale_y_log10(
"Gradient descent epochs\n(using best learning rate)")+
scale_x_continuous(
"Best validation AUC (dot=mean, segments=range over 4 random initializations)")
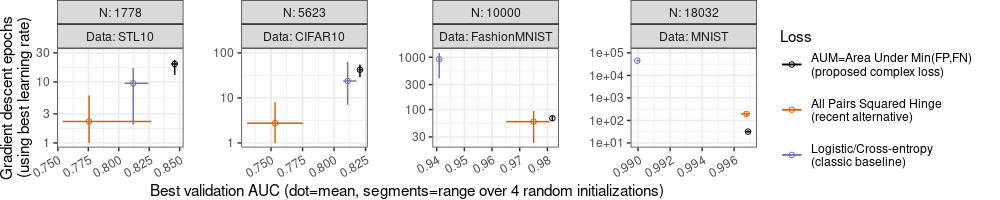
Note above how the Y axes have expanded, and now there are tick marks above the range of the data/segments, which makes the Y axis easier to read. Also the color legend has changed: I use black for the proposed method, and two other colors from Cynthia Brewer’s Dark2 palette.
Conclusions
Our goal was to explore how machine learning error/accuracy rates can be visualized, in order to compare different algorithms. We discussed various techniques for creating visualizations that make it easy for the reader to compare different algorithms.
Session info
sessionInfo()
## R Under development (unstable) (2024-11-11 r87319 ucrt)
## Platform: x86_64-w64-mingw32/x64
## Running under: Windows 11 x64 (build 22631)
##
## Matrix products: default
##
##
## locale:
## [1] LC_COLLATE=English_United States.utf8 LC_CTYPE=English_United States.utf8 LC_MONETARY=English_United States.utf8
## [4] LC_NUMERIC=C LC_TIME=English_United States.utf8
##
## time zone: America/Toronto
## tzcode source: internal
##
## attached base packages:
## [1] stats graphics utils datasets grDevices methods base
##
## other attached packages:
## [1] ggplot2_3.5.1 data.table_1.16.99
##
## loaded via a namespace (and not attached):
## [1] vctrs_0.6.5 cli_3.6.3 knitr_1.49 rlang_1.1.4 xfun_0.49 generics_0.1.3
## [7] glue_1.8.0 labeling_0.4.3 colorspace_2.1-1 scales_1.3.0 fansi_1.0.6 grid_4.5.0
## [13] munsell_0.5.1 evaluate_1.0.1 tibble_3.2.1 lifecycle_1.0.4 compiler_4.5.0 dplyr_1.1.4
## [19] RColorBrewer_1.1-3 pkgconfig_2.0.3 farver_2.1.2 R6_2.5.1 tidyselect_1.2.1 utf8_1.2.4
## [25] pillar_1.9.0 magrittr_2.0.3 tools_4.5.0 withr_3.0.2 gtable_0.3.5