The goal of this post is to explore time complexity of various methods for computing least squares regression models.

Introduction

Ordinary least squares regression is a fundamental and classic model in statistics and in machine learning. When you learn about it in a stats class, you usually see its computation via the matrix inverse, but when you look at ?lm in R you see

  method: the method to be used; for fitting, currently only ‘method =
          "qr"’ is supported...
  • Arbenz notes say that QR time complexity is O(N^3)
  • R ?solve says LAPACK dgesv is used, which says LU decomposition is used, which is same complexity as matrix multiplication, typically O(N^3) as well.
  • Note that these asymptotic time complexity statements are for N = number of columns of the design matrix X, because solve/LU/QR operates on X’X, which is a square matrix with dimensions equal to the number of columns of the design matrix X. That can be confusing, since in stats/ML we typically use N to denote the number of rows of X, and P (or D) to denote the number of columns. Both are different from the N argument to atime() which we use below for empirical estimation of the asymptotic complexity class. Are you confused yet?

So the asymptotic time complexity is the same. Why is QR preferred? For numerical stability, which means that it is more likely to compute a valid result, for numerically unusual inputs.

R implementations

Nrow <- 5
Ncol <- 2
set.seed(1)
X <- matrix(runif(Nrow*Ncol), Nrow, Ncol)
y <- runif(Nrow)
Xt <- t(X)
qres <- qr(X)
rbind(
  LU=as.numeric(solve(Xt %*% X) %*% (Xt %*% y)),
  QR=solve(qres, y),
  lm=as.numeric(coef(lm(y ~ X + 0))))

##        [,1]        [,2]
## LU 0.768795 -0.03883457
## QR 0.768795 -0.03883457
## lm 0.768795 -0.03883457

Above we see the three methods compute the same result.

Only number of rows increases with N

Converting the examples above to atime code below, (with a constant number of columns=2)

Ncol <- 2
atime.vary.rows <- atime::atime(
  setup={
    set.seed(1)
    X <- matrix(runif(N*Ncol), N, Ncol)
    y <- runif(N)
    Xt <- t(X)
    square.mat <- Xt %*% X
  },
  seconds.limit=0.1,
  mult=Xt %*% X,
  invert=solve(square.mat),
  "mult+invert"={
    as.numeric(solve(Xt %*% X) %*% (Xt %*% y))
  },
  QR={
    qres <- qr(X)
    solve(qres, y)
  },
  lm=as.numeric(coef(lm(y ~ X + 0))))

## Warning: Some expressions had a GC in every iteration; so filtering is disabled.

tit.vary.rows <- ggplot2::ggtitle(paste0(
  "Variable number of rows, N = nrow(X), ncol(X)=",Ncol))
plot(atime.vary.rows)+tit.vary.rows

## Loading required namespace: directlabels

## Warning in ggplot2::scale_y_log10("median line, min/max band"): log-10 transformation introduced infinite values.

## Warning in ggplot2::scale_y_log10("median line, min/max band"): log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.

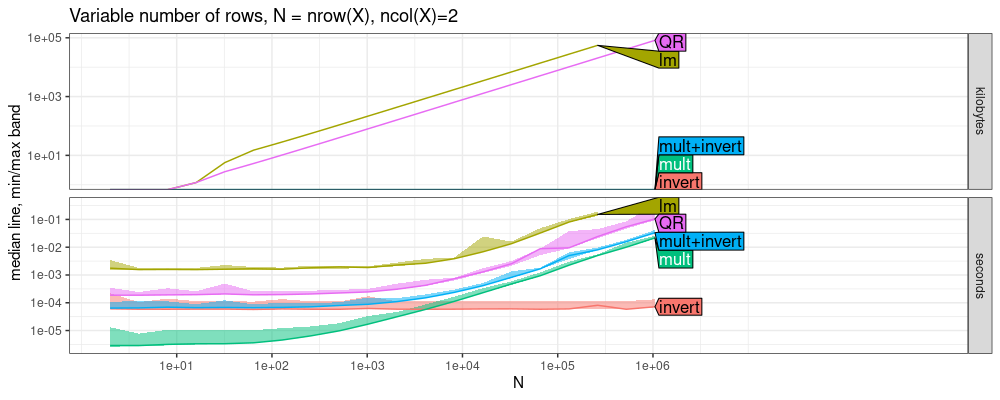
plot of chunk atime-vary-rows

The plot above shows that solve in R (LU decomposition, LAPACK dgesv) is fastest, looks like by constant factors. The code below estimates asymptotic time complexity.

refs.vary.rows <- atime::references_best(atime.vary.rows)
plot(refs.vary.rows)+tit.vary.rows

## Warning in ggplot2::scale_y_log10(""): log-10 transformation introduced infinite values.

## Warning in (function (..., deparse.level = 1) : number of rows of result is not a multiple of vector length (arg 2)

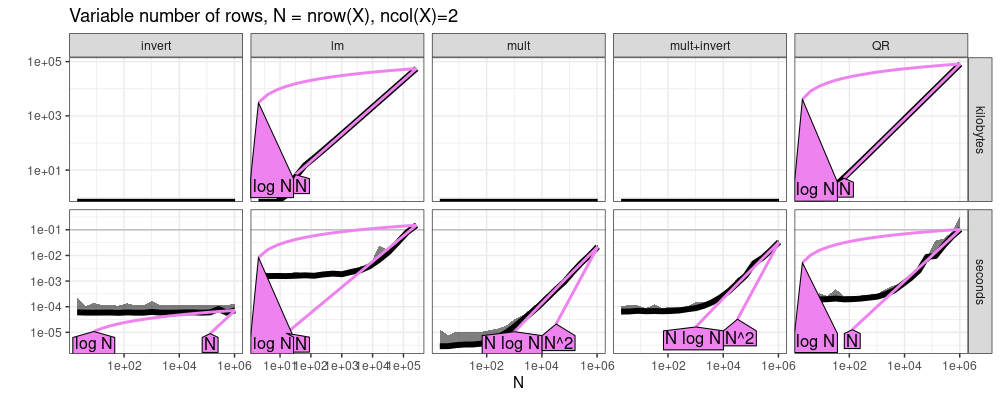
plot of chunk refs-vary-rows

The plot above shows almost linear trends for all methods, except invert is constant. Is this consistent with the cubic O(N^3) complexity which we said should be expected? Yes, because the N in O(N^3) is actually the number of columns of X, which is constant=2 in this example. So it makes sense that the matrix inversion is asymptotically constant time. The slow/linear step in the fit is actually the matrix multiplication.

Only number of columns increases, OLS/lm fit

In this section we keep the number of rows of X fixed to 100, and vary the number of columns.

Nrow <- 100
atime.vary.cols <- atime::atime(
  N=unique(as.integer(10^seq(1, log10(Nrow), l=20))),
  setup={
    set.seed(1)
    X <- matrix(runif(Nrow*N), Nrow, N)
    y <- runif(Nrow)
    Xt <- t(X)
    square.mat <- Xt %*% X
  },
  seconds.limit=0.1,
  mult=Xt %*% X,
  invert=solve(square.mat),
  "mult+invert"={
    as.numeric(solve(Xt %*% X) %*% (Xt %*% y))
  },
  QR={
    qres <- qr(X)
    solve(qres, y)
  },
  lm=as.numeric(coef(lm(y ~ X + 0))))
tit.vary.cols <- ggplot2::ggtitle(paste0(
  "Variable number of cols, N = ncol(X), nrow(X)=",Nrow))
plot(atime.vary.cols)+tit.vary.cols

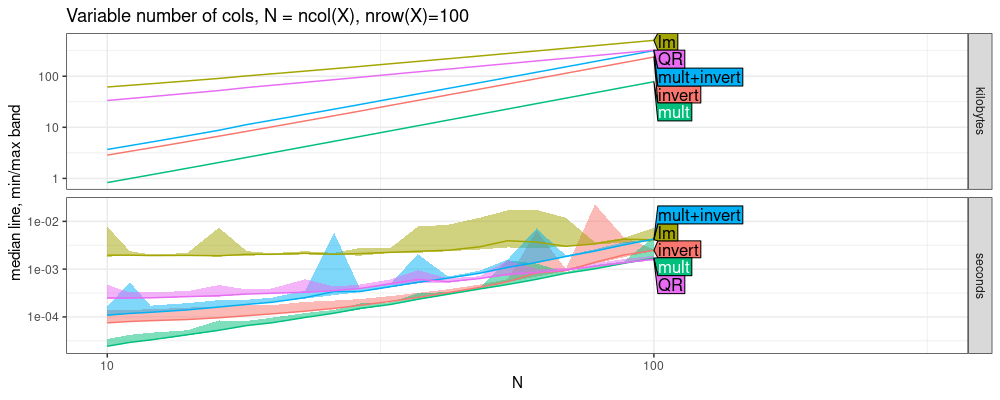
plot of chunk atime-vary-cols

The plot above shows some interesting trends, but I don’t think they should be interpreted as usual asymptotic timings plots, in which we may expect that running for a larger N would let us see lm/QR memory get smaller than LU/invert/mult. Because N is bounded by nrow(X)=r Nrow, we actually can’t run the code for any N than is already shown on the plot. The limit is because we can’t invert the X’X matrix if nrow(X)<ncol(X). In other words, if we run the same code for a larger Nrow, we get qualitatively the same result (compare memory in above and below figures).

Nrow <- 300
atime.vary.cols <- atime::atime(
  N=unique(as.integer(10^seq(1, log10(Nrow), l=20))),
  setup={
    set.seed(1)
    X <- matrix(runif(Nrow*N), Nrow, N)
    y <- runif(Nrow)
    Xt <- t(X)
    square.mat <- Xt %*% X
  },
  seconds.limit=0.1,
  mult=Xt %*% X,
  invert=solve(square.mat),
  "mult+invert"={
    as.numeric(solve(Xt %*% X) %*% (Xt %*% y))
  },
  QR={
    qres <- qr(X)
    solve(qres, y)
  },
  lm=as.numeric(coef(lm(y ~ X + 0))))
tit.vary.cols <- ggplot2::ggtitle(paste0(
  "OLS variable number of cols, N = ncol(X), nrow(X)=",Nrow))
plot(atime.vary.cols)+tit.vary.cols

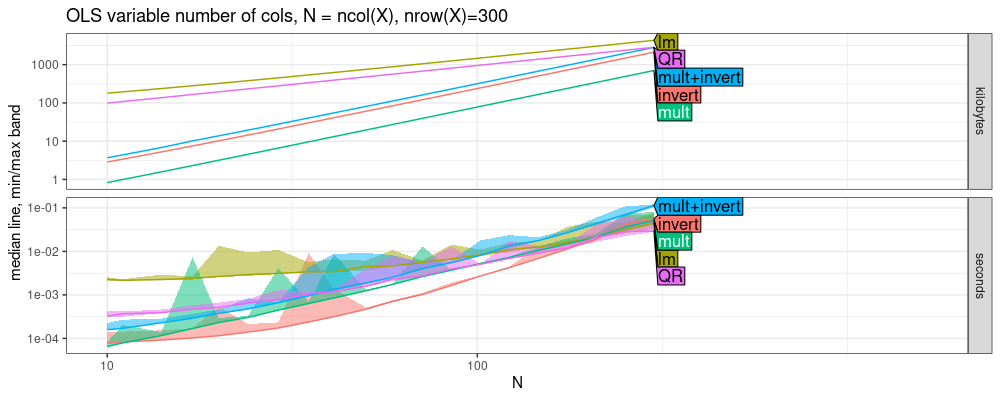
plot of chunk atime-vary-cols-larger

Only vary number of columns with ridge regression

To get past the limitation of the previous section, we can use a ridge regression fit (L2 regulariztion), so any number of columns can be used with any number of rows.

Nrow <- 100
atime.vary.cols.ridge <- atime::atime(
  setup={
    set.seed(1)
    X <- matrix(runif(Nrow*N), Nrow, N)
    y <- runif(Nrow)
    Xt <- t(X)
    square.mat <- Xt %*% X + diag(N)
  },
  seconds.limit=0.1,
  mult=Xt %*% X,
  invert=solve(square.mat),
  "mult+invert"={
    as.numeric(solve(Xt %*% X+diag(N)) %*% (Xt %*% y))
  },
  QR={
    qres <- qr(X)
    solve(qres, y)
  },
  lm.ridge=as.numeric(coef(MASS::lm.ridge(y ~ X + 0, lambda=1))))
tit.vary.cols.ridge <- ggplot2::ggtitle(paste0(
  "Ridge variable number of cols, N = ncol(X), nrow(X)=",Nrow))
plot(atime.vary.cols.ridge)+tit.vary.cols.ridge

## Warning in ggplot2::scale_y_log10("median line, min/max band"): log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.

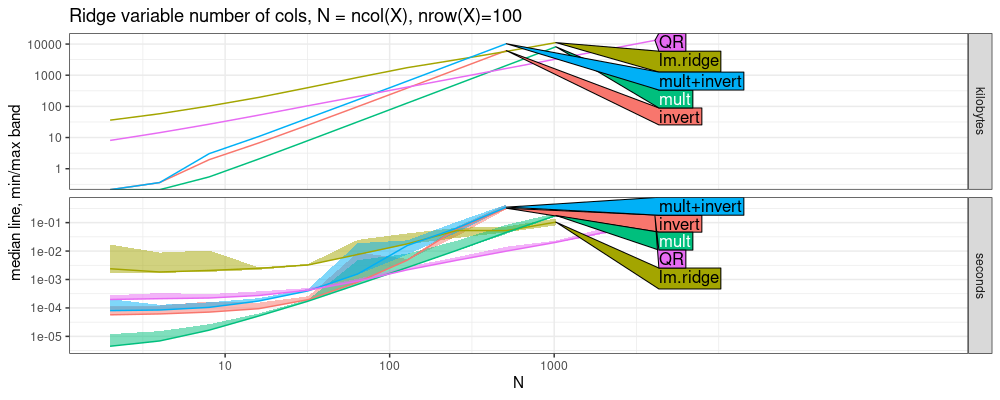
plot of chunk atime-vary-cols-ridge

The plot above shows some very interesting trends

  • QR is fastest, and has smallest slope, same as lm.ridge.
  • next largest slope is mult.
  • largest slopes are LU and invert. Below we estimate the asymptotic complexity classes.
refs.vary.cols.ridge <- atime::references_best(atime.vary.cols.ridge)
plot(refs.vary.cols.ridge)+tit.vary.cols.ridge

## Warning in ggplot2::scale_y_log10(""): log-10 transformation introduced infinite values.

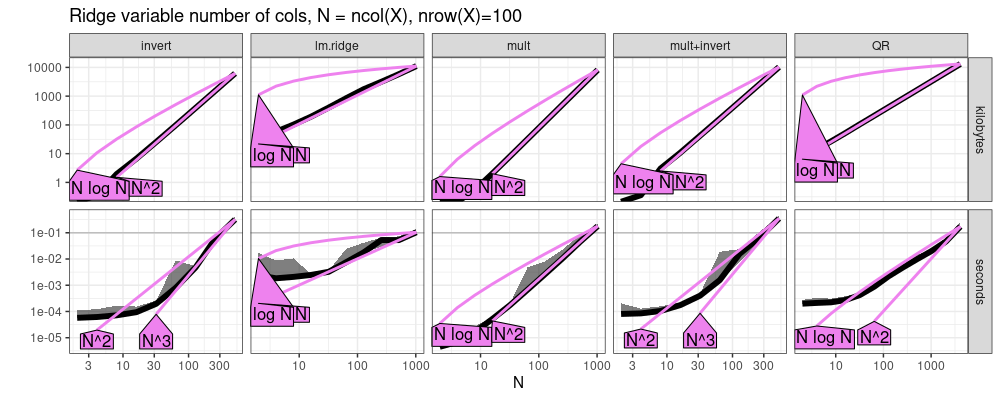
plot of chunk refs-vary-cols-ridge

The plot above suggests the following asymptotic complexity classes, as a function of ncol(X).

  • lm.ridge and QR are linear.
  • mult is quadratic.
  • invert and LU are cubic.

Both rows and columns increase with N

The code below additionally increases the number of columns.

atime.vary.rows.cols <- atime::atime(
  setup={
    set.seed(1)
    X <- matrix(runif(N*N), N, N)
    y <- runif(N)
    Xt <- t(X)
    square.mat <- Xt %*% X 
  },
  seconds.limit=0.1,
  mult=Xt %*% X,
  invert=solve(square.mat),
  "mult+invert"={
    as.numeric(solve(Xt %*% X) %*% (Xt %*% y))
  },
  QR={
    qres <- qr(X)
    solve(qres, y)
  },
  lm=as.numeric(coef(lm(y ~ X + 0))))
tit.vary.rows.cols <- ggplot2::ggtitle(
  "Variable number of rows and cols, N = nrow(X) = ncol(X)")
plot(atime.vary.rows.cols)+tit.vary.rows.cols

## Warning in ggplot2::scale_y_log10("median line, min/max band"): log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.
## log-10 transformation introduced infinite values.

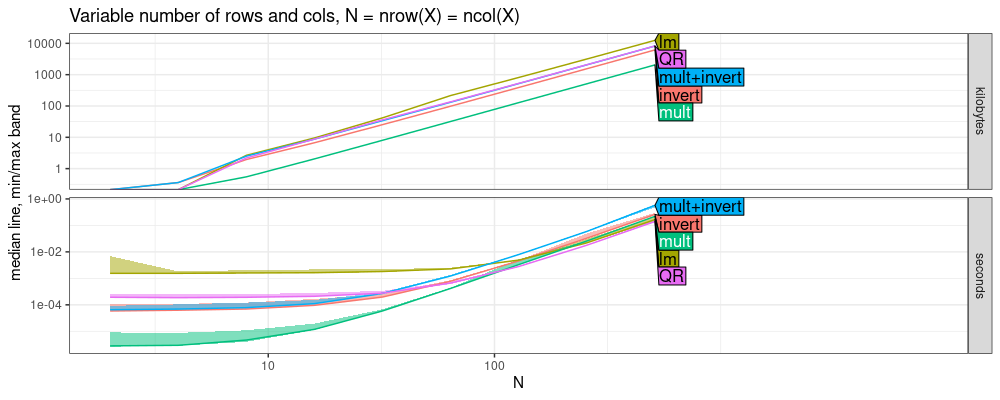
plot of chunk atime-vary-rows-cols

The plot above shows that QR and lm are about the same, which makes sense, because lm uses QR decomposition method. The difference between them for small N can be attributed to the overhead of the lm formula parsing, etc. Both are slightly faster than LU in this case. Below we estimate asymptotic complexity classes.

refs.vary.rows.cols <- atime::references_best(atime.vary.rows.cols)
plot(refs.vary.rows.cols)+tit.vary.rows.cols

## Warning in ggplot2::scale_y_log10(""): log-10 transformation introduced infinite values.

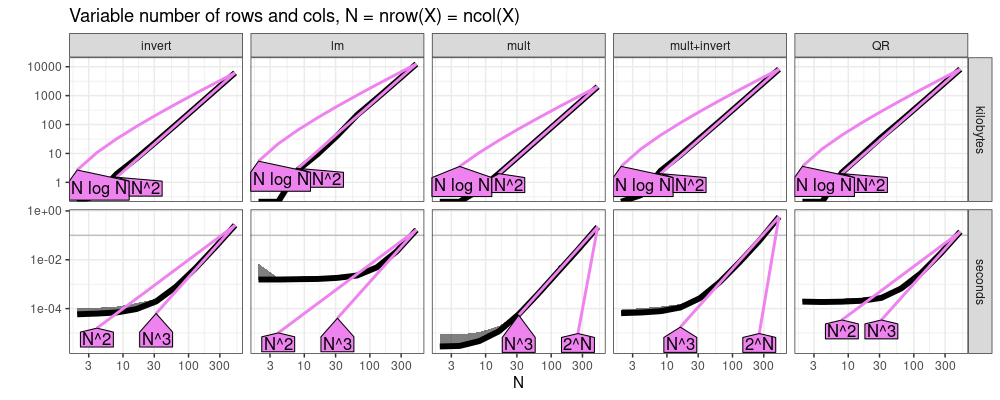
plot of chunk refs-vary-rows-cols

The plot above suggests cubic N^3 asymptotic time for all methods, and quadratic N^2 asymptotic memory.

Synthesis

Overall our empirical analysis suggests the following time complexity classes for nrow(X)=N, ncol(X)=P, and M=min(N,P) (rank of X).

operation P constant N constant vary M=N=P
lm O(N) O(P) O(M^3)
QR solve O(N) O(P) O(M^3)
mult O(N) O(P^2) O(M^3)
invert O(1) O(P^3) O(M^3)
mult+invert O(N) O(P^3) O(M^3)

Is any method clearly faster?

  • with lots of data and few features (N>P), all methods are fast/linear (P constant column).
  • with lots of features and few data (N<P), lm/QR decomposition is asymptotically faster than matrix multiply and solve/invert/LU (N constant column).

Conclusions

We have shown that there are some asymptotic time/memory differences, between the different methods of estimating ordinary least squares regression coefficients.

Session info

sessionInfo()

## R version 4.4.1 (2024-06-14 ucrt)
## Platform: x86_64-w64-mingw32/x64
## Running under: Windows 11 x64 (build 22631)
## 
## Matrix products: default
## 
## 
## locale:
## [1] LC_COLLATE=English_United States.utf8  LC_CTYPE=English_United States.utf8    LC_MONETARY=English_United States.utf8
## [4] LC_NUMERIC=C                           LC_TIME=English_United States.utf8    
## 
## time zone: America/Toronto
## tzcode source: internal
## 
## attached base packages:
## [1] stats     graphics  utils     datasets  grDevices methods   base     
## 
## loaded via a namespace (and not attached):
##  [1] directlabels_2024.1.21 vctrs_0.6.5            cli_3.6.3              knitr_1.48             rlang_1.1.4           
##  [6] xfun_0.47              highr_0.11             bench_1.1.3            generics_0.1.3         data.table_1.16.99    
## [11] glue_1.7.0             nc_2024.9.20           colorspace_2.1-1       scales_1.3.0           fansi_1.0.6           
## [16] quadprog_1.5-8         grid_4.4.1             evaluate_0.24.0        munsell_0.5.1          tibble_3.2.1          
## [21] MASS_7.3-60.2          profmem_0.6.0          lifecycle_1.0.4        compiler_4.4.1         dplyr_1.1.4           
## [26] pkgconfig_2.0.3        atime_2024.8.8         farver_2.1.2           lattice_0.22-6         R6_2.5.1              
## [31] tidyselect_1.2.1       utf8_1.2.4             pillar_1.9.0           magrittr_2.0.3         withr_3.0.1           
## [36] tools_4.4.1            gtable_0.3.5           ggplot2_3.5.1