Indirect reverse dependencies
For a recent grant proposal submission to the National Science
Foundation POSE program, I wanted to make an argument that the
data.table R package is one of the most used, out of all R
packages.
I therefore wrote some code to compute the number of indirect reverse dependencies for all R packages. First, download meta-data from the current CRAN,
library(data.table)
if(!file.exists("packages.rds")){
u <- paste0(
"https://cloud.r-project.org/web/packages/packages.rds")
download.file(u, "packages.rds")
}
packages <- readRDS("packages.rds")
pkg.dt <- data.table(packages)[is.na(Path)]
nrow(pkg.dt)
## [1] 18761
The output above shows the number of packages on CRAN.
Direct reverse imports
Then, we can get direct reverse imports,
imp.by <- pkg.dt[, .(
imported.by=strsplit(`Reverse imports`, ", ")[[1]]
), by=.(Imports=Package)]
imp.by[!is.na(imported.by)]
## Imports imported.by
## <char> <char>
## 1: abc ecolottery
## 2: abc poems
## 3: ABCanalysis EDOtrans
## 4: abind agroclim
## 5: abind alleHap
## ---
## 79416: ztable rrtable
## 79417: ztable webr
## 79418: zyp fasstr
## 79419: zyp FlowScreen
## 79420: zyp gimms
The table above contains one row for each direct reverse import listed on CRAN.
imp.by[Imports=="data.table"]
## Imports imported.by
## <char> <char>
## 1: data.table accessibility
## 2: data.table actel
## 3: data.table ActivePathways
## 4: data.table ActivityIndex
## 5: data.table ADAMgui
## ---
## 1323: data.table yaps
## 1324: data.table youngSwimmers
## 1325: data.table zebu
## 1326: data.table zeitgebr
## 1327: data.table zoomGroupStats
The table above contains a row for each direct reverse import listed
for the data.table package.
Indirect reverse imports
Then, we can use a loop to recursively compute indirect reverse imports,
order.i <- 0
ord.dt.list <- list()
order.pkgs <- pkg.dt[, .(Package, Imports=Package)]
while(nrow(order.pkgs)){
print(order.i <- order.i+1)
order.deps <- imp.by[
order.pkgs,
on="Imports", nomatch=0L, allow.cartesian=TRUE]
if(nrow(order.deps)){
ord.dt.list[[order.i]] <- data.table(order.i, order.deps)
}
order.pkgs <- unique(order.deps[, .(Package, Imports=imported.by)])
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10
## [1] 11
## [1] 12
## [1] 13
## [1] 14
## [1] 15
## [1] 16
## [1] 17
(ord.dt <- do.call(rbind, ord.dt.list))
## order.i Imports imported.by Package
## <num> <char> <char> <char>
## 1: 1 A3 <NA> A3
## 2: 1 AATtools <NA> AATtools
## 3: 1 ABACUS <NA> ABACUS
## 4: 1 abbreviate <NA> abbreviate
## 5: 1 abbyyR <NA> abbyyR
## ---
## 2107718: 15 immcp <NA> rlang
## 2107719: 15 nlmixr2plot nlmixr2 rlang
## 2107720: 16 nlmixr2 <NA> cli
## 2107721: 16 nlmixr2 <NA> glue
## 2107722: 16 nlmixr2 <NA> rlang
The table above contains one row for each reverse import (direct or
indirect). Direct reverse imports have order.i=1 and indirect have
larger values.
Below we check that the number of packages in this table is the same as the number of packages in the CRAN meta-data,
rbind(pkgs.in.ord=length(unique(ord.dt$Package)), pkgs=nrow(pkg.dt))
## [,1]
## pkgs.in.ord 18761
## pkgs 18761
The output above indicates that the table of reverse imports was computed correctly (the total number of packages is correct).
Subset of packages funded by NSF
Which packages were funded by NSF?
pkg.dt[, Desc.no.newlines := gsub("\n\\s+", " ", Description)]
(nsf.pkgs <- pkg.dt[
grep("NSF|National Science Foundation", Desc.no.newlines),
Package])
## [1] "adaptivetau" "BAS" "bizicount"
## [4] "fastCorrDiff" "fdapace" "fields"
## [7] "futureheatwaves" "hurricaneexposure" "hwep"
## [10] "LatticeKrig" "melt" "merDeriv"
## [13] "metagear" "mined" "mixtools"
## [16] "mosaic" "mosaicData" "MultNonParam"
## [19] "nonnest2" "PHInfiniteEstimates" "PST"
## [22] "RealVAMS" "rEMM" "rmonad"
## [25] "SPlit" "SPREDA" "stream"
## [28] "supercompress" "TAG" "telefit"
## [31] "tensr"
Which of the reverse imports were funded by NSF?
dt.pkgs <- ord.dt[Package=="data.table", imported.by]
(int.pkgs <- intersect(nsf.pkgs, dt.pkgs))
## [1] "bizicount" "fdapace" "futureheatwaves"
## [4] "hurricaneexposure"
The output above shows that there are four reverse imports that were also funded by NSF.
Computing path from reverse import in dependency graph
What is the path of packages from each reverse import in the dependency graph?
select.dt <- data.table(
rev.dep=int.pkgs,
imported.by=int.pkgs,
Package="data.table")
path.dt.list <- list()
iteration <- 0
while(nrow(select.dt)){
print(iteration <- iteration+1)
dep.dt <- ord.dt[select.dt, on=.(imported.by, Package)]
path.dt.list[[iteration]] <- dep.dt
select.dt <- dep.dt[
Imports != Package,
.(rev.dep, imported.by=Imports, Package)]
}
## [1] 1
## [1] 2
## [1] 3
## [1] 4
(path.dt <- do.call(rbind, path.dt.list)[
order(Package, rev.dep, -order.i),
.(Package, rev.dep, order.i, imported.by, Imports)])
## Package rev.dep order.i imported.by Imports
## <char> <char> <num> <char> <char>
## 1: data.table bizicount 4 bizicount DHARMa
## 2: data.table bizicount 3 DHARMa gap
## 3: data.table bizicount 2 gap plotly
## 4: data.table bizicount 1 plotly data.table
## 5: data.table fdapace 2 fdapace Hmisc
## 6: data.table fdapace 1 Hmisc data.table
## 7: data.table futureheatwaves 1 futureheatwaves data.table
## 8: data.table hurricaneexposure 1 hurricaneexposure data.table
The table above shows that there are two direct reverse imports
(futureheatwaves, hurricaneexposure) for which the path length (max
order.i) is 1. The fdapace package imports Hmisc which imports
data.table (path length 2), whereas bizicount imports DHARMa
which imports gap which imports plotly which imports data.table
(path length 4).
Unique reverse imports, direct or all
The code below counts the number of unique reverse imports (either direct or all), for each CRAN package,
(dep.type.counts <- rbind(
data.table(dep.type="all", max.order=Inf),
data.table(dep.type="direct", max.order=1)
)[, {
ord.dt[order.i <= max.order, .(
rev.imports=length(unique(na.omit(imported.by)))
), by=Package
][, `:=`(
rank=rank(-rev.imports),
prop.bigger=1-rank(rev.imports)/.N
)][order(rank)]
}, by=dep.type])
## dep.type Package rev.imports rank prop.bigger
## <char> <char> <int> <num> <num>
## 1: all magrittr 8638 1.0 0.000000e+00
## 2: all rlang 8469 2.0 5.330206e-05
## 3: all Rcpp 8413 3.0 1.066041e-04
## 4: all glue 8275 4.0 1.599062e-04
## 5: all R6 8011 5.0 2.132083e-04
## ---
## 37518: direct ztpln 0 11616.5 6.191301e-01
## 37519: direct zTree 0 11616.5 6.191301e-01
## 37520: direct ztype 0 11616.5 6.191301e-01
## 37521: direct ZVCV 0 11616.5 6.191301e-01
## 37522: direct zzlite 0 11616.5 6.191301e-01
The data.table package appears near the top in terms of number of
dependent packages,
(dt.counts <- dep.type.counts[Package=="data.table"])
## dep.type Package rev.imports rank prop.bigger
## <char> <char> <int> <num> <num>
## 1: all data.table 2663 45 0.0023452908
## 2: direct data.table 1327 11 0.0005330206
The table above shows that data.table has
- 1326 direct reverse imports, which is rank 11 among CRAN packages (only 10 other packages, 0.05% of all CRAN packages, have a larger number of reverse imports).
- 2661 packages which import either directly or indirectly, which is rank 45 among CRAN packages (only 44 other packages, 0.2% of all CRAN packages, have a larger number).
Comparison with other CRAN packages
The code below can be used to compute a histogram of reverse import
counts, among all CRAN packages. To compute a histogram using a
data.table rolling join, we first need to look at the range of the
data, and then use the min/max to define the sequence of midpoints of
histogram bins.
log10(range(dep.type.counts$rev.imports))
## [1] -Inf 3.936413
log10.min <- 0
log10.max <- 4
(bin.dt <- data.table(
log10.bin=c(-Inf,seq(log10.min, log10.max, by=0.5))
)[, bin := 10^log10.bin][, Bin := round(bin)][])
## log10.bin bin Bin
## <num> <num> <num>
## 1: -Inf 0.000000 0
## 2: 0.0 1.000000 1
## 3: 0.5 3.162278 3
## 4: 1.0 10.000000 10
## 5: 1.5 31.622777 32
## 6: 2.0 100.000000 100
## 7: 2.5 316.227766 316
## 8: 3.0 1000.000000 1000
## 9: 3.5 3162.277660 3162
## 10: 4.0 10000.000000 10000
The bins defined above range from 1 to 10000 on the log scale, with an additional bin for 0 (packages that have no reverse imports). Below we use a rolling join to figure out which packages are closest to each bin midpoint on the log scale,
dep.type.counts[, log10.rev.imports := log10(rev.imports)]
(bin.log.join <- bin.dt[dep.type.counts, .(
dep.type, Package, Bin, bin,
log10.bin=x.log10.bin,
log10.rev.imports),
roll="nearest",
on=.(log10.bin=log10.rev.imports)])
## dep.type Package Bin bin log10.bin log10.rev.imports
## <char> <char> <num> <num> <num> <num>
## 1: all magrittr 10000 10000 4 3.936413
## 2: all rlang 10000 10000 4 3.927832
## 3: all Rcpp 10000 10000 4 3.924951
## 4: all glue 10000 10000 4 3.917768
## 5: all R6 10000 10000 4 3.903687
## ---
## 37518: direct ztpln 0 0 -Inf -Inf
## 37519: direct zTree 0 0 -Inf -Inf
## 37520: direct ztype 0 0 -Inf -Inf
## 37521: direct ZVCV 0 0 -Inf -Inf
## 37522: direct zzlite 0 0 -Inf -Inf
The table above has columns for bin midpoint on the log scale,
log10.bin, as well as the actual number of reverse imports,
log10.rev.imports. We can compute a histogram by summarizing for
each bin,
(bin.log.hist <- bin.log.join[, .(
n.packages=.N
), by=.(dep.type, bin)])
## dep.type bin n.packages
## <char> <num> <int>
## 1: all 10000.000000 18
## 2: all 3162.277660 45
## 3: all 1000.000000 68
## 4: all 316.227766 111
## 5: all 100.000000 211
## 6: all 31.622777 379
## 7: all 10.000000 673
## 8: all 3.162278 1394
## 9: all 1.000000 1572
## 10: all 0.000000 14290
## 11: direct 3162.277660 5
## 12: direct 1000.000000 16
## 13: direct 316.227766 58
## 14: direct 100.000000 117
## 15: direct 31.622777 276
## 16: direct 10.000000 642
## 17: direct 3.162278 1481
## 18: direct 1.000000 1876
## 19: direct 0.000000 14290
The table above has a column n.packages which shows the number of
packages which are closest to each bin. These numbers can be plotted
to compare with the corresponding number of reverse imports for the
data.table package,
library(ggplot2)
ggplot()+
theme_bw()+
geom_line(aes(
bin, n.packages),
color="grey50",
size=2,
data=bin.log.hist)+
geom_vline(aes(
xintercept=rev.imports),
data=dt.counts)+
geom_text(aes(
rev.imports*0.9, Inf,
label=sprintf(paste(
"data.table rev. imports=%d",
"rank=%d/%d packages",
"%.2f%% of packages have",
"larger rev. dep. count",
sep="\n"),
rev.imports, rank, nrow(pkg.dt), prop.bigger*100)),
data=dt.counts,
hjust=1,
vjust=1.1)+
facet_grid(. ~ dep.type, labeller=label_both)+
scale_y_log10(paste(
"Number of packages with that",
"reverse dependency count (log scale)",
sep="\n"))+
scale_x_log10(paste(
"Reverse dependency count",
"(number of other packages which import, log scale)"))
## Warning: Transformation introduced infinite values in continuous x-
## axis
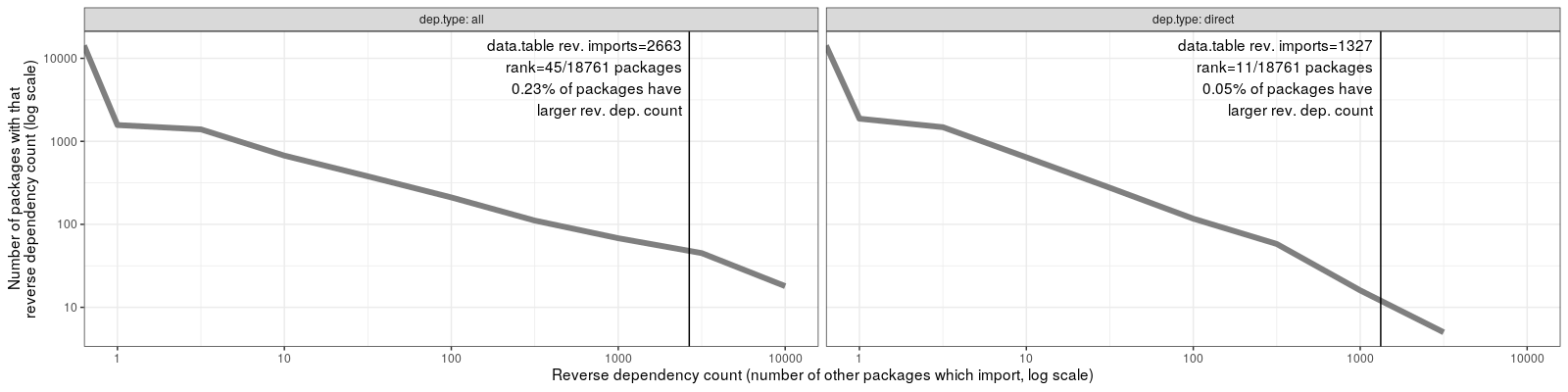
The figure above shows that data.table is ranked near the top, when
comparing with other CRAN packages in terms of number of reverse
imports.
Appendix: rolling join in original or log space?
In the code above, to compute a histogram that we want to display in the log space, we did a rolling join in the log space, which results in symmetric histogram bins. If we did the join in the original space, then the histogram bins would have been asymmetric, as the code below shows,
bin.tall <- melt(
bin.dt[bin>0],
measure.vars=c("log10.bin", "bin"),
id.vars=c("Bin", "log10.bin"))
bin.tall[, next.break := c(value+c(diff(value)/2,NA)), by=variable]
bin.tall[, next.log10 := ifelse(
variable=="bin", log10(next.break), next.break)]
bin.tall[, prev.log10 := c(NA, next.log10[-.N]), by=variable]
bin.tall[, distance := ifelse(variable=="bin", "original", "log")]
bin.not.na <- bin.tall[!(is.na(prev.log10)|is.na(next.log10))]
ggplot()+
geom_segment(aes(
prev.log10, distance,
xend=next.log10, yend=distance),
data=bin.not.na)+
geom_point(aes(
log10.bin, distance),
data=bin.not.na)+
facet_grid(. ~ Bin, labeller=label_both, scales="free")+
scale_x_continuous(breaks=seq(log10.min, log10.max, by=0.1))

The figure above shows the center of each histogram bin as a dot, and the min/max extent of each bin as a line segment. It is clear that using original space distances for the join results in bins which are asymmetric, in the sense that the bin will count more data which is larger than the bin center.
Another way of looking at it is empirically, in terms of the reverse imports data,
bin.log.join[, log10.diff := ifelse(
log10.rev.imports == -Inf, 0, log10.rev.imports-log10.bin)]
bin.width <- 0.05
ggplot()+
geom_histogram(aes(
log10.diff, after_stat(ncount)),
binwidth=bin.width,
data=bin.log.join)+
scale_x_continuous(breaks=seq(-1, 1, by=0.2))+
geom_point(aes(x,y),data=data.table(x=0,y=0))+
facet_grid(dep.type ~ Bin, labeller=label_both)
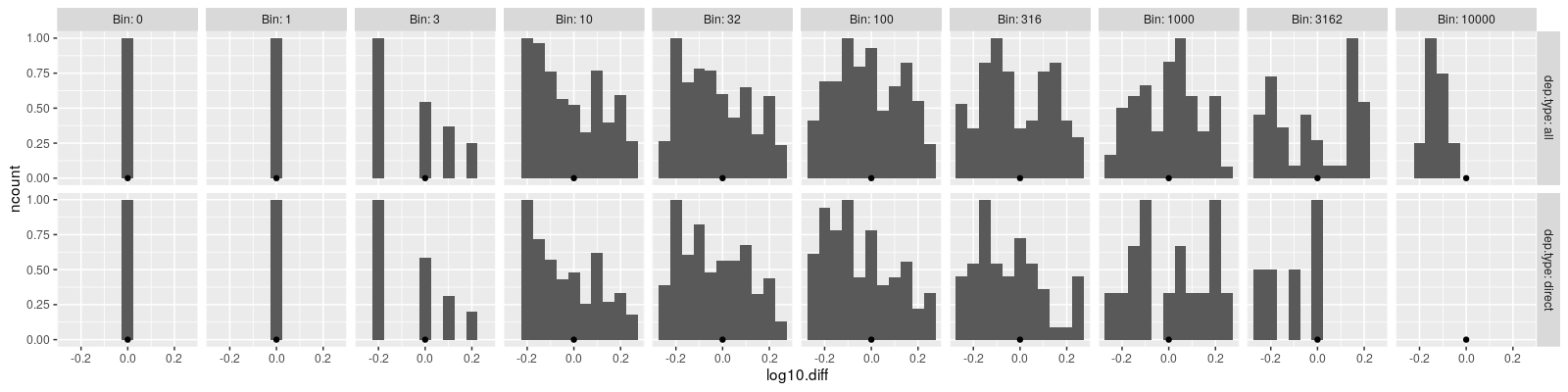
The histogram above shows the distribution of differences between the
actual number of reverse imports and the corresponding bin
center. Most of the differences fall between -0.2 and 0.2, which is to
be expected, since bin.dt used a bin size of 0.5 on the log scale.
What if we did the same computation using the original distance scale?
bin.join <- bin.dt[dep.type.counts, .(
dep.type, Package, Bin,
log10.bin=x.log10.bin,
rev.imports),
roll="nearest",
on=.(bin=rev.imports)
][, log10.rev.imports := log10(rev.imports)
][, log10.diff := ifelse(
log10.rev.imports == -Inf, 0, log10.rev.imports-log10.bin)]
ggplot()+
geom_histogram(aes(
log10.diff, after_stat(ncount)),
binwidth=bin.width,
data=bin.join)+
scale_x_continuous(breaks=seq(-1, 1, by=0.2))+
geom_point(aes(x,y),data=data.table(x=0,y=0))+
facet_grid(dep.type ~ Bin, labeller=label_both)
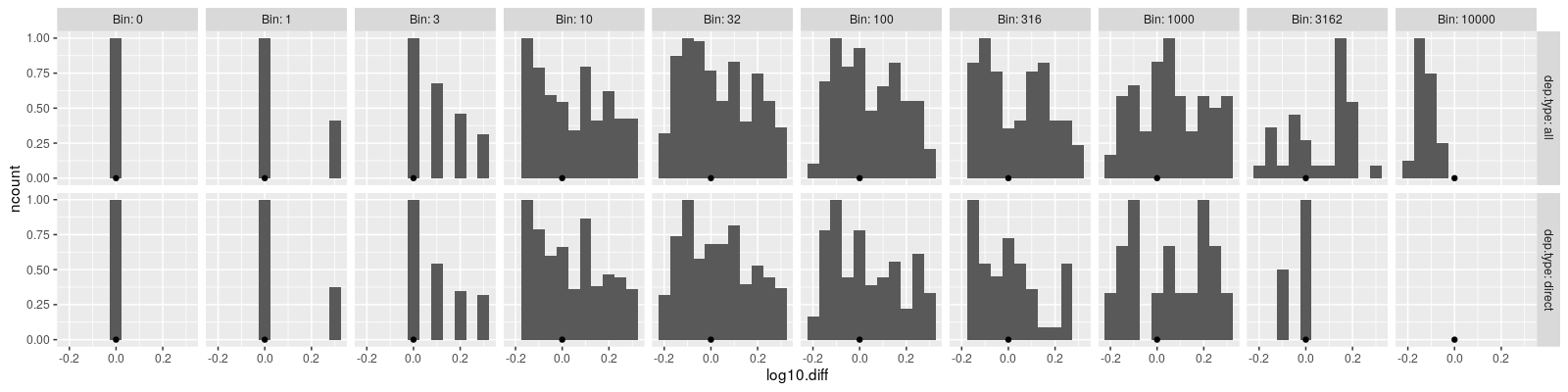
The bin assignments above were computed using a rolling join in the original reverse import count space (not the log space), so each histogram above is skewed to the right (the are more larger differences in each bin), as expected based on our theoretical analysis above which showed the asymmetric bins.
Finally we can compare the two histograms in the same plot. First we combine the two data sets created from rolling joins,
joinDT <- function(DT, distance, sign){
DT[, .(distance, sign, log10.diff, dep.type, Bin)]
}
(bin.both.join <- rbind(
joinDT(bin.join, "original", -1),
joinDT(bin.log.join, "log", sign=1)))
## distance sign log10.diff dep.type Bin
## <char> <num> <num> <char> <num>
## 1: original -1 -0.06358680 all 10000
## 2: original -1 -0.07216787 all 10000
## 3: original -1 -0.07504911 all 10000
## 4: original -1 -0.08223200 all 10000
## 5: original -1 -0.09631327 all 10000
## ---
## 75040: log 1 0.00000000 direct 0
## 75041: log 1 0.00000000 direct 0
## 75042: log 1 0.00000000 direct 0
## 75043: log 1 0.00000000 direct 0
## 75044: log 1 0.00000000 direct 0
Then we compute histograms ourselves in the code below using the
hist function (instead of using geom_histogram as we did in the
code above),
max.abs.diff <- 0.4
breaks.vec <- seq(-max.abs.diff, max.abs.diff, by=bin.width)
(bin.both.hist <- bin.both.join[, {
hlist <- hist(log10.diff, breaks.vec, plot=FALSE)
with(hlist, data.table(log10.diff=mids, ncount=counts/max(counts)))
}, by=.(distance, sign, dep.type, Bin)])
## distance sign dep.type Bin log10.diff ncount
## <char> <num> <char> <num> <num> <num>
## 1: original -1 all 10000 -0.375 0
## 2: original -1 all 10000 -0.325 0
## 3: original -1 all 10000 -0.275 0
## 4: original -1 all 10000 -0.225 0
## 5: original -1 all 10000 -0.175 1
## ---
## 604: log 1 direct 0 0.175 0
## 605: log 1 direct 0 0.225 0
## 606: log 1 direct 0 0.275 0
## 607: log 1 direct 0 0.325 0
## 608: log 1 direct 0 0.375 0
The table above contains histograms of differences between actual
numbers of reverse imports, and the corresponding bin centers. The
ncount column is normalized between 0 and 1 so that the histograms
can be displayed on a common scale. In the code below we also compute
the mean of the differences, to see if there is any skew to larger
values than the bin center, as we would expect.
(bin.both.stats <- dcast(
bin.both.join,
distance + sign + dep.type + Bin ~ .,
list(length, mean),
value.var = "log10.diff"))
## distance sign dep.type Bin log10.diff_length log10.diff_mean
## <char> <num> <char> <num> <int> <num>
## 1: log 1 all 0 14290 0.000000000
## 2: log 1 all 1 1572 0.000000000
## 3: log 1 all 3 1394 -0.057402270
## 4: log 1 all 10 673 -0.024827086
## 5: log 1 all 32 379 -0.029358816
## 6: log 1 all 100 211 -0.013584970
## 7: log 1 all 316 111 -0.013580821
## 8: log 1 all 1000 68 -0.004673764
## 9: log 1 all 3162 45 -0.017145384
## 10: log 1 all 10000 18 -0.132331020
## 11: log 1 direct 0 14290 0.000000000
## 12: log 1 direct 1 1876 0.000000000
## 13: log 1 direct 3 1481 -0.066554348
## 14: log 1 direct 10 642 -0.039676030
## 15: log 1 direct 32 276 -0.038371816
## 16: log 1 direct 100 117 -0.048097463
## 17: log 1 direct 316 58 -0.042129331
## 18: log 1 direct 1000 16 0.007191530
## 19: log 1 direct 3162 5 -0.102999626
## 20: original -1 all 0 14290 0.000000000
## 21: original -1 all 1 2217 0.087579769
## 22: original -1 all 3 858 0.091649620
## 23: original -1 all 10 625 0.039381623
## 24: original -1 all 32 347 0.030125174
## 25: original -1 all 100 197 0.038456067
## 26: original -1 all 316 102 0.035174080
## 27: original -1 all 1000 74 0.058778621
## 28: original -1 all 3162 34 0.061689482
## 29: original -1 all 10000 17 -0.128054947
## 30: original -1 direct 0 14290 0.000000000
## 31: original -1 direct 1 2581 0.082226326
## 32: original -1 direct 3 908 0.086368755
## 33: original -1 direct 10 562 0.032615799
## 34: original -1 direct 32 249 0.031694090
## 35: original -1 direct 100 103 0.028964698
## 36: original -1 direct 316 48 0.004440089
## 37: original -1 direct 1000 17 0.053739484
## 38: original -1 direct 3162 3 -0.027134169
## distance sign dep.type Bin log10.diff_length log10.diff_mean
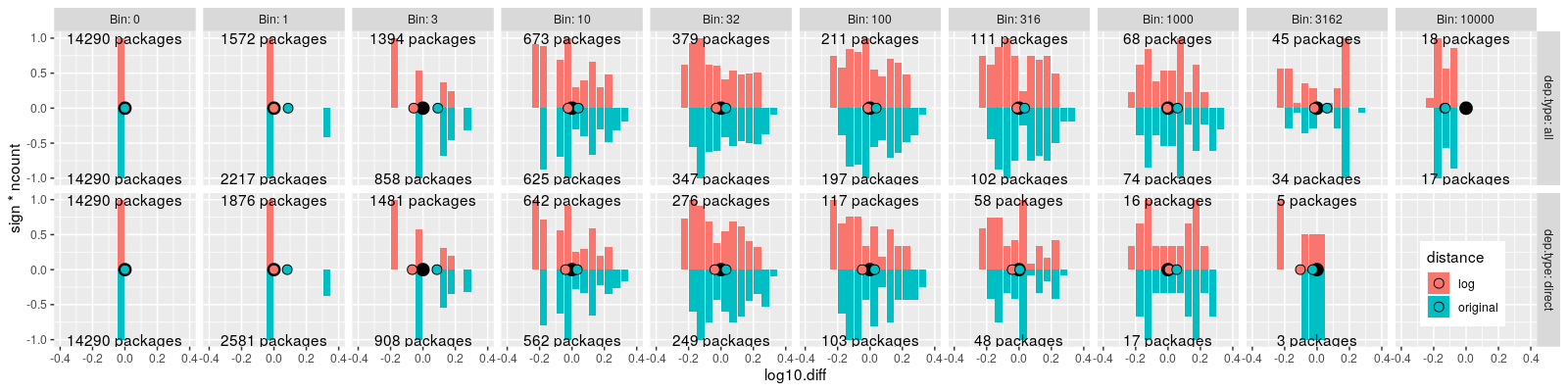
The table above has number of packages and mean difference columns, for every bin/histogram to plot, which we show below,
ggplot()+
theme(legend.position=c(0.95, 0.2))+
geom_bar(aes(
log10.diff, sign*ncount, fill=distance),
stat="identity",
data=bin.both.hist)+
geom_text(aes(
0, sign, label=sprintf(
"%d packages", log10.diff_length)),
data=bin.both.stats)+
geom_point(aes(
x,y),
size=4,
data=data.table(x=0,y=0))+
geom_point(aes(
log10.diff_mean, 0, fill=distance),
data=bin.both.stats,
size=3,
shape=21)+
facet_grid(dep.type ~ Bin, labeller=label_both)